인공지능에 쓰이는? 선형대수3

행렬식 응용

사다리꼴 행렬의 행렬식

사다리꼴 행렬(대각선 아래 또는 위가 완전 0인 행렬)의 행렬식은 대각선 성분을 전부 곱한 것과 같다. 이는 유도를 해보면 쉽게 알수있는데, 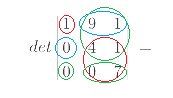이렇게 생긴 행렬이 있다하면 이렇게 한 개 빼고 전부 0인 행이나 열을 기준으로 계산하면 되고, 그 0이 아닌 수는 사다리꼴 행렬의 특성상 대각선에 위치해 있으므로 자연스럽게 대각선 수만 곱하게 되는 것이다.

행렬식 계산

• A 행렬에서 행만 바꾸는 계산으로 B 행렬을 만들었을 때 B의 행렬식은 A 행렬식x(-1) 이다.
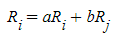• 이런 식의 행 연산으로 A행렬에서 행렬 B를 만들었을 때 B의 행렬식은 (a)xA 행렬식 이다.

고유값과 고유벡터

동차 선형시스템과 행렬식

지난 시간에 행렬식 AX=B에서 A의 역행렬이 존재하면 해는 무조건 한개이고, 존재하지 않으면 해는 무한하거나 없다고 배웠다. 또한 이를 응용하여 동차 선형시스템 AX=0에서 A의 역행렬이 존재하면 해는 무조건 한개-즉 역행렬-, 존재하지 않으면 해는 무한하다고도 했다. 이제 행렬식으로 역행렬의 존재 여부를 알 수 있으므로 AX=0을 다시 들여다보면…

• A의 행렬식이 0이면 역행렬이 존재하지 않으므로 X는 무한하다.
• A의 행렬식이 0이 아니면 역행렬이 존재하므로 X는 영행렬(0)이다.

이를 반대로 생각해볼 수도 있다.

• AX=0의 해가 0밖에 없으면 A의 행렬식은 0이 아니다.
• AX=0의 해가 무한하면 A의 행렬식은 0이다.

이를 사용해 벡터들의 선형독립 여부를 판단할 수 있다. 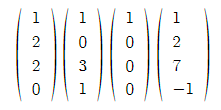위 네 개의 벡터가 선형 독립, 즉 세개의 벡터로 나머지 하나 벡터를 만들 수 있는지 여부는 지난시간에 말했던 것처럼 동차 선형시스템을 사용하면 된다. 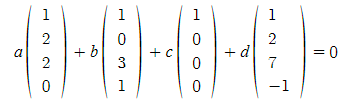즉 이렇게 말이다. 원리는 간단하게 왼쪽 네개 중 하나를 우변으로 옮기고 계수로 나누면 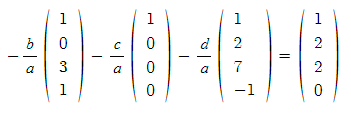이런 식으로 나머지 벡터로 하나의 벡터를 만드는 식이 성립되기 때문이다.

여기서 중요한 점은, 저번에 또 말했듯이 a,b,c,d가 전부 0밖에 안되면 선형독립이라 했다. 이 식을 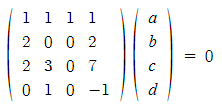이렇게 행렬식으로도 표현할 수 있는데 여기서 a~d 행렬이 유일한 해 0이면 선형독립이 성립하므로 우리는 저 4x4 행렬의 행렬식을 계산하여 선형독립 여부를 계산할 수 있다.

요약하자면 AX=0 꼴로 만들기->A의 행렬식 계산->행렬식이 0이 아니면 선형독립 인 것이다.

고유값과 고유벡터

NxN 행렬 A와 Nx1 행렬 X가 주어질 때, 상수 L(람다)를 사용해 AX=LX으로 표현할 수 있으면 그 수 L은 고유값이라고 한다. 즉 복잡한 행렬연산을 상수 곱셈 하나로 단순화시키는 것이다.

만약 X=0이라면 L은 무한하겠다. 이건 당연하니까 우리는 X!=0에서의 L을 찾는 것이다.

일단 양쪽의 행과 열 수를 맞춰줘야 하므로 l을 LI(I는 고유행렬)로 하여 대각 성분이 L인 NxN 대각행렬로 바꿔준다. 그러면 AX=LIX가 될 텐데, 이는 (A-LI)X=0 으로도 나타낼 수 있다. 엥, 이건 동차 선형시스템이잖아!

그렇다. 여기서는 위와 반대로 X가 0이 아니여야 하므로 (A-LI)의 행렬식이 0이면 X가 무한히 있겠다는 성질을 활용하는 것이다.

이 L을 A의 고유값(eigenvalue)라고 부른다. 그리고 L을 구했으니 위 식에 집어넣으면 X도 구할 수 있는데, 이때의 X를 고유벡터(eigenvector)라고 한다.

(A-LI)의 행렬식=0은 L의 N차방정식으로 나타내어지므로 L은 최대 N개 존재할 수 있다. 없을 수도 있고…

정사각 행렬의 대각행렬화

NxN 행렬 A가 있고, 마찬가지로 NxN인 역행렬이 존재하는 행렬 P와 대각행렬(대각성분 빼고 다 0인 행렬) D가 있으면 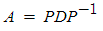즉 A를 P 곱하기 D 곱하기 P의 역행렬 로 나타낼 수 있는지의 문제이다. 이는 다시 말해 A에서 P와 D를 구할 수 있느냐의 문제이기도 하다.

이를 수행하려면 우선 A가 N개의 선형 독립인 고유벡터들을 가지고 있어야 한다. 만일 A의 고유벡터들이 N개이지 않거나 선형 독립이지 않으면 A는 대각행렬화할 수 없다. 이 고유벡터들이 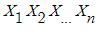이렇게 있으면 P는 이 고유벡터들로 구성된 행렬이다. 즉 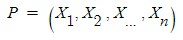이렇게 된다는 말이다(X1,X2,…은 열 하나에 해당됩니다) 그리고 X1,…,Xn일 때의 고유값을 각각 L1,L2,…,Ln 이라 하면 D는 이렇게 고유값들로 구성된 대각행렬 이 된다.

참고로 N개의 고유벡터들이 선형 독립인지를 아는 쉬운 방법은 당연하게도, (A-LI)의 행렬식=0이 N개의 서로 다른 해를 가지고 있으면 된다. 만일 3x3 행렬인데 고유값이 2개인 등의 경우는 고유벡터들을 계산해 선형 독립 여부를 직접 알아봐야 한다.

대칭행렬의 대각행렬화

대칭 행렬(A와 A^T(행과 열을 뒤바꾼것)이 일치하는 행렬)은 더 쉽게 대각화할 수 있다. NxN인 대칭행렬 A는 무조건 N개의 고유값들을 가지고, 고유벡터의 값도 고유벡터의 노름(norm-벡터의 거리 ∥x∥, 각 벡터 요소들을 제곱하여 더한 뒤 제곱근해서 구한다)=1이기 때문에 구할 수 있다.

대각행렬화를 하면 편리한 점이 있는데, 대표적으로 행렬의 제곱이 있다. 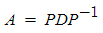일 때 A를 m제곱하면 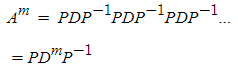이렇게 나온다. 여기서 D는 대각행렬이라 m제곱의 값은 대각 요소들에 m제곱을 해준 것과 같기 때문에 결국 계산이 매우 단순해진다!