인공지능에 쓰이는? 선형대수2

벡터와 행렬식

벡터

선형대수에서 벡터(정확히는 열벡터)는 열이 하나뿐인 행렬을 의미한다. 즉 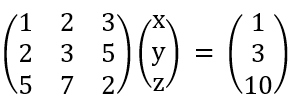여기서 x,y,z 행렬과 1,3,10은 벡터이다. 이때 행의 개수를 벡터의 차원이라고 말한다. 따라서 여기서는 3차원 벡터

벡터의 선형결합

같은 차원 내의 벡터는 서로 합쳐 새로운 벡터를 구성할 수 있고, 그 반대도 마찬가지이다. 이를 선형결합이라고 한다. 수식으로 나타내면 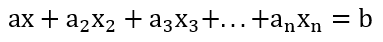b 벡터는 x,x2,...,xn 벡터들의 실수배 합으로 구성될 수 있다는 것이다.(a,a2,…,an은 실수)

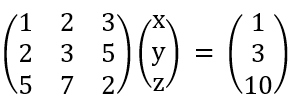위 그림도 벡터의 선형결합으로 표현할 수 있는데, 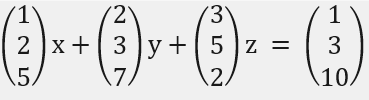바로 이렇게 되는 것이다. (1,3,10) 벡터를 위 세 벡터로 표현할 수 있는지는 x,y,z값을 구할수 있나 없나에 따라 갈릴 것이다. 이 값은 이전에 소개한 연립방정식으로 구하면 된다.

선형독립

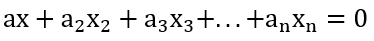이렇게 생긴 선형결합에서(이 식은 동차 선형시스템을 선형식으로 변환한 것이기도 하다. 실수 a~an이 모여서 벡터를, 벡터 x~xn이 모여서 행렬을 구성한다.) 정답이 a,a2,...,an이 0이 되는 경우밖에 없을 때 벡터 x~xn을 각각 선형독립이라고 한다. 다르게 말하자면 x~xn 벡터는 다 같이 0을 곱하지 않는 한 모여서 영벡터가 될 수 없다는 것이다.

또 다르게 말하자면, 위 식은 ax=-a2x2-a3x3-...-anxn 이렇게도 표현할 수 있는데 a~an이 0이 되는 것 외에는 식이 성립되지 않으므로 이 벡터들은 각 벡터가 다른 벡터들로 표현할 수 없다는 말이기도 하다.

선형독립인지 아닌지는 위 식을 다시 행렬화(AX=B)한 뒤 A 행렬의 행렬식을 통해 구할 수 있다.

행렬식

역행렬

역행렬도 중고등학교 시간에 배웠듯이 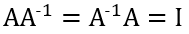곱했을 때 단위행렬이 되는 행렬 A^-1을 역행렬이라 한다.

모든 행렬이 역행렬을 가지지는 아니다.

역행렬을 구하는 방법은 AX=I 라는 식을 놓고 연립방정식을 풀면 된다. 만일 해가 존재하지 않으면 행렬 A는 역행렬이 존재하지 않는다. 컴퓨터의 힘을 빌려 연립방정식을 풀어보면 이렇게 구할 수 있다. 푸는 방법이 전에 설명한 것과 조금 다른데, 일단 넘어가자.

행렬식

AX=B 에서 A의 역행렬은 중요한 의미를 갖는다. 만약 A의 역행렬이 존재하면 X는 무조건 한개이고 A의 역행렬이 존재하지 않으면 X는 무수히 많거나 없다.

그럼 동차 선형시스템 AX=0에서는? A의 역행렬이 존재하면 X는 무조건 한개이나 X=0*(A^-1), 즉 0(영행렬)이 되겠고, A의 역행렬이 존재하지 않으면 X는 무수히 많거나 없겠지만 동차 선형시스템에서는 해가 무조건 존재해야 하므로 X는 무수히 많다.

이 역행렬이 존재하나, 존재하지 않나 여부는 행렬식을 통해 알 수 있다.

행렬식은 단순히 그 행렬에서 나오는 고유값인데, 행렬식을 구하는 방법은 조금 설명하기 복잡하므로 이 사이트나, 이 강의를 들어보는 것이 좋겠다.

아무튼 중요한 점은, 행렬식이 0이면 그 행렬은 역행렬이 존재하지 않고, 행렬식이 0이 아니면 그 행렬은 역행렬이 존재한다는 것이다.