인공지능에 쓰이는? 선형대수1
인공지능 선형대수-행렬
선형대수?
최근 LG AI연구원에서 주최하는 인공지능 프로그램에서 교육을 받고 있다. 문제는 해당 강좌를 전혀 못알아먹고 있다는 것이다.. 학부생 시절 인공지능 기초강좌나 수학 지식은 다 배웠건만, 그게 몇년 전의 일이라 다 까먹어버려… 다행히 당직과 같은 사람들을 위한 공개강좌가 인터넷에 나와있고, 전공책도 아직 버리지 않아서 선형대수를 다시 복습할 수 있었다. 따라 이번 글은 선형대수를 더이상 까먹지 않도록 쓰는 목적도 있다.
선형대수란
(KOOC의 《AI 비전공자를 위한 기초 수학》을 참조했습니다.)
선형대수는 말 그대로 선형적인 것을 다루는 학문이다. 여기서 선형적인 것이란 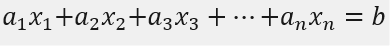 이렇게 직선으로 표현할 수 있는 것을 의미한다. 물론 x 말고 y,z,… 등이 있을 수도 있다. 여기에서 a는 실수일 수 있고 심지어 함수일수도 있으나 사인값/코싸인값 같은거면 직선이 아니기 때문에 선형이 아니다.
이렇게 직선으로 표현할 수 있는 것을 의미한다. 물론 x 말고 y,z,… 등이 있을 수도 있다. 여기에서 a는 실수일 수 있고 심지어 함수일수도 있으나 사인값/코싸인값 같은거면 직선이 아니기 때문에 선형이 아니다.
선형대수학에서 가장 핵심은 행렬과 벡터이다.
행렬
행렬의 기본 연산은 중고등학교 시간에 배웠기 때문에 제외한다. 다만 하나 추가로 배워놓을 연산은 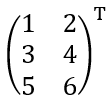 T 연산인데, 이는 각 값의 행과 열을 바꾸는 연산을 의미한다. 즉
T 연산인데, 이는 각 값의 행과 열을 바꾸는 연산을 의미한다. 즉 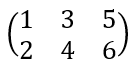 이렇게 되는 것이다.
이렇게 되는 것이다.
식을 행렬로 나타내기
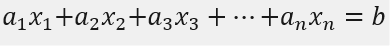 이걸 다시 보면 이 식은 행렬로 나타낼 수 있다! 바로 행렬의 곱셈을 사용하면 된다.
이걸 다시 보면 이 식은 행렬로 나타낼 수 있다! 바로 행렬의 곱셈을 사용하면 된다. 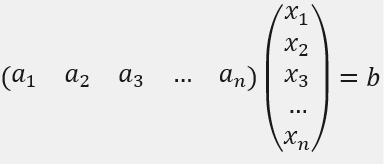 바로 이렇게 말이다.
바로 이렇게 말이다. 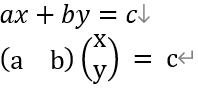 마찬가지로 변수가 여러개면 위와 같이 표현할 수도 있겠다.
마찬가지로 변수가 여러개면 위와 같이 표현할 수도 있겠다.
연립방정식
식을 행렬화해서 푸는 가장 유명한 방법은 연립방정식이 아닐가 싶다. 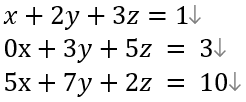 이렇게 된 식이 있을 때, 이를 행렬로 표현해보면
이렇게 된 식이 있을 때, 이를 행렬로 표현해보면  이렇게 된다. 이제 맨 왼쪽의 행렬을 위 사다리꼴 행렬로 만들어 처리해야 한다.
이렇게 된다. 이제 맨 왼쪽의 행렬을 위 사다리꼴 행렬로 만들어 처리해야 한다.
위 사다리꼴 행렬은  이런 식으로 행렬의 대각선 아래가 전부 0인 행렬을 의미한다. 반대로는 대각선 위가 전부 0인 아래 사다리꼴 행렬이 있다.
이런 식으로 행렬의 대각선 아래가 전부 0인 행렬을 의미한다. 반대로는 대각선 위가 전부 0인 아래 사다리꼴 행렬이 있다.  참고로 대각선 요소에 0이 있어도 사다리꼴 행렬이다. 중요한 것은 대각선 아래와 위가 전부 0이라는 것이다.
참고로 대각선 요소에 0이 있어도 사다리꼴 행렬이다. 중요한 것은 대각선 아래와 위가 전부 0이라는 것이다. 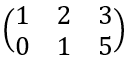 이렇게 정사각꼴이 아닌 행렬은? 이것도 사다리꼴 행렬이 맞다. 대각선은 행과 열 번호가 같음을 의미하기 때문이다.
이렇게 정사각꼴이 아닌 행렬은? 이것도 사다리꼴 행렬이 맞다. 대각선은 행과 열 번호가 같음을 의미하기 때문이다.
어쨌든 위 사다리꼴 행렬을 만들기 위해 다음과 같은 방법을 사용한다. 1. 행렬을 간략화한다. 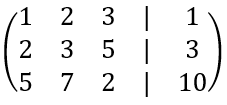 이렇게 모든 행렬을 하나로 합친 뒤 x,y,z 변수 대신 그 자리에 직선(|)을 긋는다. 이를 첨가행렬이라 한다. 2. 행렬을 위 사다리꼴 행렬화한다. 이 때 두 가지 법칙을 사용한다.
이렇게 모든 행렬을 하나로 합친 뒤 x,y,z 변수 대신 그 자리에 직선(|)을 긋는다. 이를 첨가행렬이라 한다. 2. 행렬을 위 사다리꼴 행렬화한다. 이 때 두 가지 법칙을 사용한다.
- 각 행을 교체하는 방법
- 해당 행의 정수배에 다른 행을 정수배한 것을 더하는 방법 즉 각 행을 R1,R2,R3이라 하면 R2 = aR1 + bR2 이렇게 표현할 수 있는 것이다. 이때 a는 0이 되어서는 안된다.
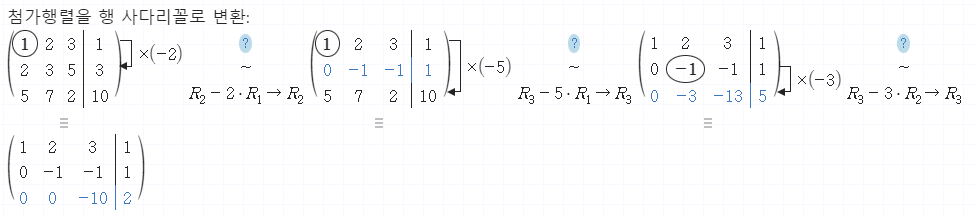 이런 식으로 계산이 진행되는 것이다.
이런 식으로 계산이 진행되는 것이다.  따라서 사다리꼴화 된 행렬은 이렇게 나올 것이다. 이를 다시 식으로 표현하면
따라서 사다리꼴화 된 행렬은 이렇게 나올 것이다. 이를 다시 식으로 표현하면 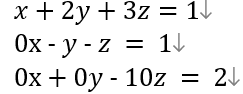 이렇게 될 것이다. 이제 z를 바로 구할 수 있으니 x와 y를 구하면 된다.
이렇게 될 것이다. 이제 z를 바로 구할 수 있으니 x와 y를 구하면 된다.
여기서 재밌는 점은, 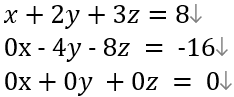 이렇게 행의 계수와 값이 전부 0이 되어버리는 해가 있으면 이 식은 해가 무한하게 많아진다. 이럴 때는 z값을 특정 상수 t로 칭하고 x와 y의 연립방정식을 풀면 된다. 즉 x+2y = 8-3t -4y = -16+8t 이 되는 것이다.
이렇게 행의 계수와 값이 전부 0이 되어버리는 해가 있으면 이 식은 해가 무한하게 많아진다. 이럴 때는 z값을 특정 상수 t로 칭하고 x와 y의 연립방정식을 풀면 된다. 즉 x+2y = 8-3t -4y = -16+8t 이 되는 것이다.
반대로 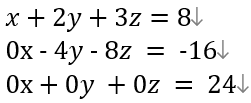 행의 계수가 전부 0인데 값이 있는 것이 있으면 이 식은 성립될 수 없다.
행의 계수가 전부 0인데 값이 있는 것이 있으면 이 식은 성립될 수 없다.
동차 선형시스템
이제부터 방정식에서의 계수 행렬을 A, 변수 행렬을 X, 값 행렬을 B 라고 하겠다. 즉 위 예제에서의 연립방정식 행렬은 AX=B 이렇게 표현할 수 있는 것이다. 
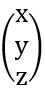
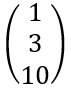 위에서부터 차례대로 A, X, B
위에서부터 차례대로 A, X, B
이때 B가 영행렬(모든 요소가 0인 행렬)이면 이 행렬은 동차 선형시스템(호모지니어스 시스템homogeneous system)이라고 한다.
동차 선형시스템의 중요한 점은 무조건 해가 있다라는 것이다. 문제는 이 해가 한개뿐인지, 무한히 많은지는 A행렬을 봐야 알 수 있는데, 이는 다음에 설명하겠다.