Post

알고리듬 문제를 풀어보자-정렬

Posted
By Kaebal Kim
12 min read
알고리듬 문제를 풀어보자-정렬

정렬 알고리듬

코딩 테스트를 준비하면서 문자열 정렬을 정리해봐야할 것 같아 정리해보게 되었다.

정렬에 사용될 문자열은 (1,4,3,6,5,2) 로 정의하고, 정렬은 오름차순으로 한다.

삽입정렬(Insertion Sort)

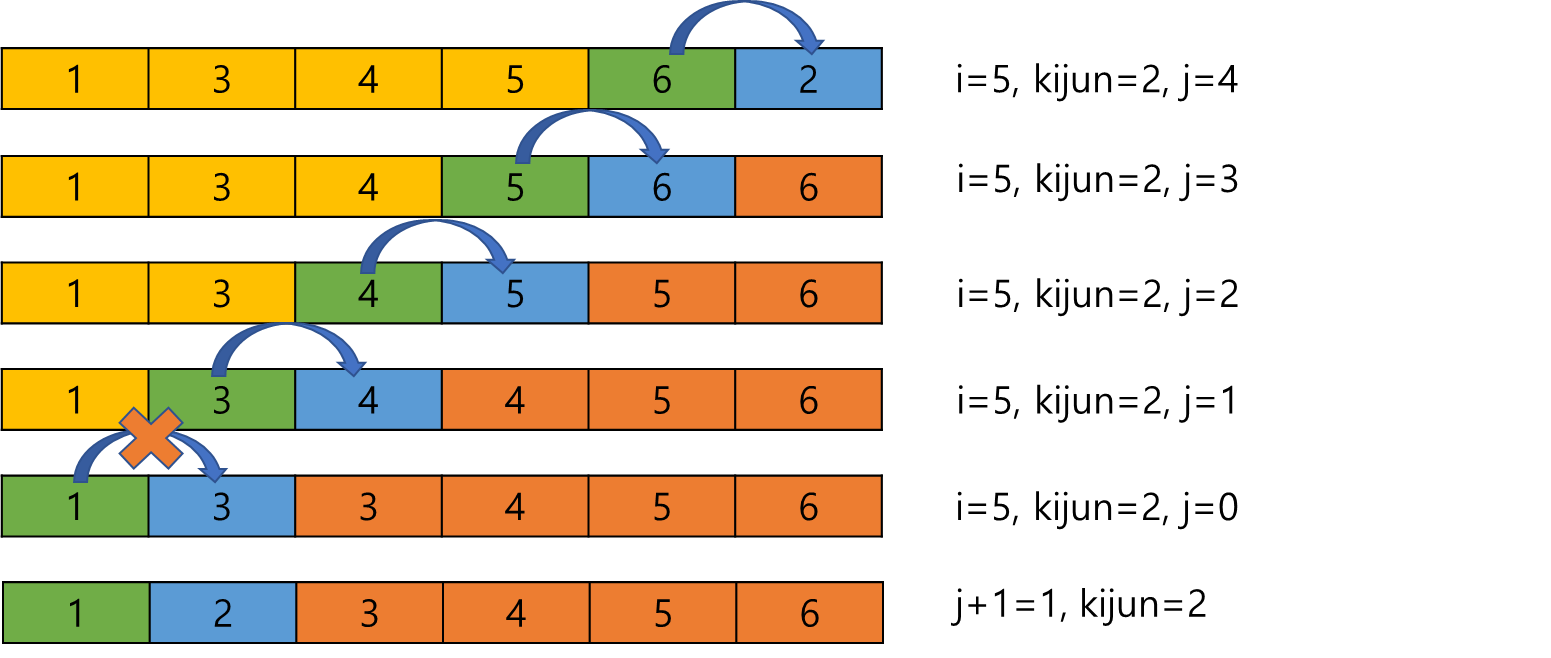
2번째 인덱스(A[1]) 부터 시작하여, 해당 인덱스의 문자와 그 앞의 인덱스 문자들을 차례대로 비교하여 더 작으면 위치를 바꾼다. 이를 인덱스가 끝날때까지 반복한다.

즉 반복문을 이중으로 수행한다.

  • 한번은 기준 문자를 정하는 반복문
  • 나머지는 기준 문자와 그 앞의 인덱스 문자들을 비교하는 내부 반복문

(1,4,3,6,5,2)를 예시로 들면 아래 그림과 같다.

참 간단하다!
그러나 이는 (5,4,3,2,1) 같이 (오름차순 기준)역순이 많은 문자열에서는 매번 내부 반복문을 끝까지 돌려야 하므로 정렬 시간이 많이 든다는 단점이 있다.

코드로 표현

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

#include <iostream>
#include <vector>

using namespace std;

int main(){
    // 입력받는 부분
    int n;
    cin>>n;
    vector<int> tosso(n);
    for(int i=0;i<n;i++){
        cin>>tosso[i];
    }
    
    // 기준문자를 정하는 반복문
    for(int i=1;i<n;i++){
        int kijun=tosso[i];
        int j;
        // 앞의 인덱스들과 비교하는 반복문
        for(j=i-1; j>=0; j--){
          // 작을 경우
          if(tosso[j]>kijun){
            // 해당 문자를 한칸 오른쪽으로 밀기
            tosso[j+1] = tosso[j];
          }
          // 아닌 경우 넘어가기
          else{
              break;
          }
        }
        // 오른쪽으로 밀었으므로 비어있는 칸(끝났을 때의 j+1 인덱스)에 기준문자 넣기
        // 안밀었을 경우에는 j+1=i이므로 동일
        tosso[j+1] = kijun;
    }
    
    for(int i=0;i<n;i++){
        cout<<tosso[i]<<endl;
    }
    return 0;
}

코드로 구현할때는 순서를 일일이 바꾸기에는 코드가 복잡해지므로
한칸씩 옆으로 민 다음 내부반복이 끝나면 그때의 앞인덱스+1에 기준문자를 넣는 방법을 사용하였다.
사실 이게 삽입정렬(민 다음 빈칸에 기준문자를 넣으니)이라는 말에 더 맞을수도?

초록색은 j(앞 인덱스), 파란색은 j+1이다!

병합정렬(Merge Sort)

병합 정렬은 나누고 합치기(디바이드 앤드 콘쿼-D&C) 방법을 사용하는 대표적인 알고리듬이다.

나누고 합치기(Divide and Conquer)

나누고 합치기 방법은 이후에 나올 동적 계획법에도 쓰이는 중요한 방법이다.

  • 문제를 여러 부분 문제로 나눈다.(디바이드)
    • 즉 (1,2,3,4,5,6)을 정렬하는 문제를 (1,2,3) 정렬/(4,5,6) 정렬 이렇게 나누는 형식이다.
  • 부문 문제를 재귀적으로 푼다.(콘쿼)
    • 부문 문제의 크기가 충분히 작으면 그냥 푼다. 즉 (1) 정렬/(2,3) 정렬 이런 문제는 그냥 푸는 방식이다.
  • 푼 부분 문제들을 합친다.(병합)

방법

위 나누고 합치기 방법을 적용하면 이와 같이 풀 수 있겠다. 일단 원리만 이야기하자면

  • 배열을 완전히 절반으로 나눈다. 만약 홀수이면 1/2, 3/4 이렇게(n/2)
  • 재귀를 사용해 나뉜 두 배열을 정렬한다.
  • 두 배열을 병합해 하나의 배열로 다시 합친다.

여기서 정렬하고 병합하는 방법은 다음과 같다.

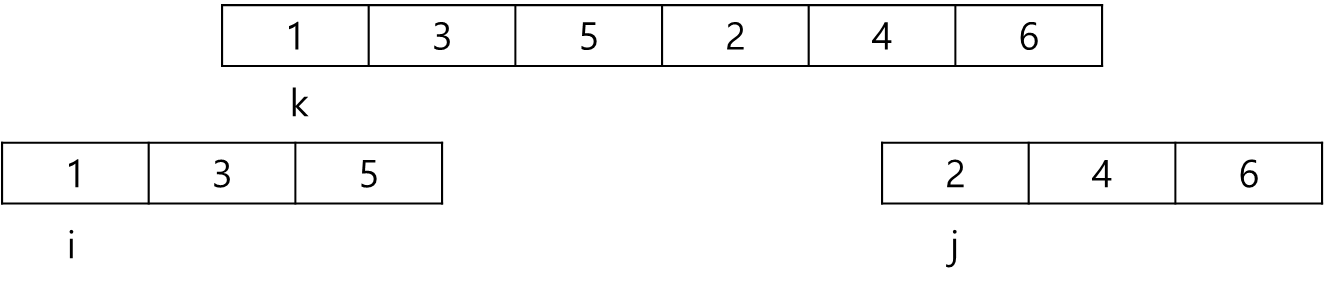
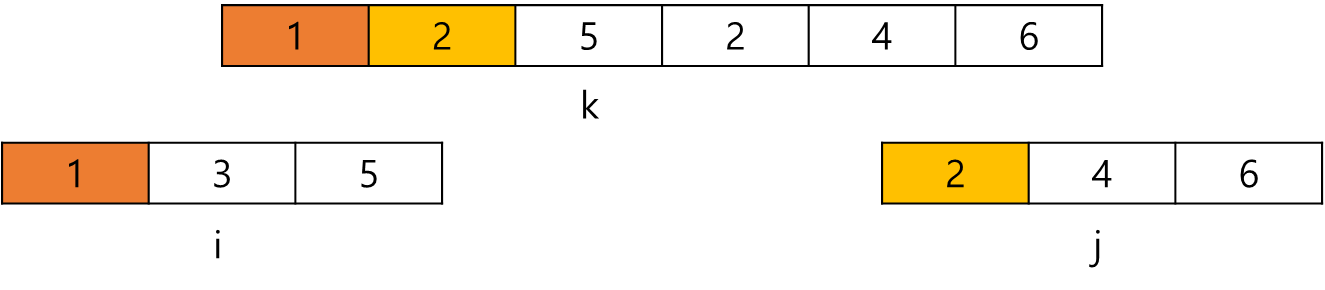
이렇게 나뉜 배열이 있다. 주의할 점으로 나뉜 배열은 정렬되어 있어야 한다.

이렇게 왼쪽 인덱스(i), 오른쪽 인덱스(j), 기준 인덱스(kijun-k)를 각자의 맨 앞으로 초기화한다.

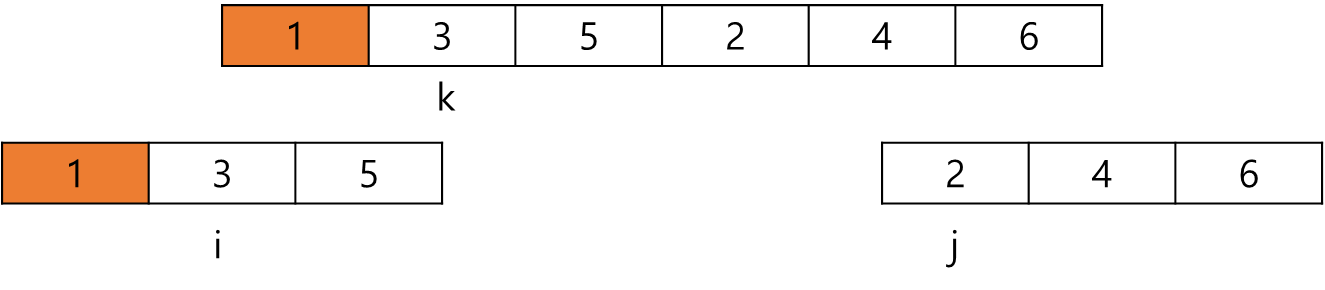
그다음 i와 j 인덱스를 비교해 둘 중 작은 것을 k에다 넣는다.
그리고 k 및 i,j 중 넣은 쪽을 다음 인덱스로 이동한다.

즉 여기서는 i(1)을 넣었으므로 i를 다음 인덱스(3)로 이동한다.

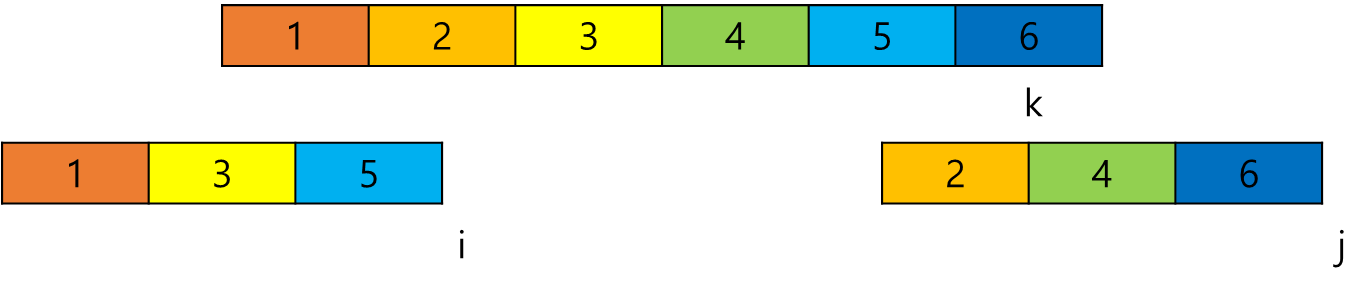
그다음 이를 계속 반복한다. 이번에는 i(3)과 j(2)를 비교하므로 j가 k에 넣어질 것이고, j와 k의 인덱스를 증가시킨다.
만약 둘중 하나의 인덱스가 끝나면 나머지를 그대로 끝에 집어넣으면 된다.

최종적으로는 이렇게 될 것이다.

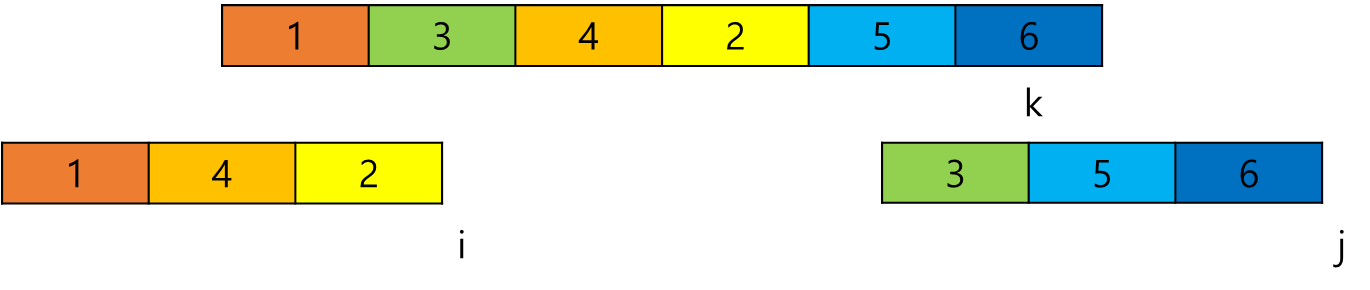
그런데 이전에 말했듯이 나눈 배열이 정렬이 되어있지 않으면

이렇게 되어버린다.(과정은 한번 생각해보시길)

즉 어떻게든 나눈 배열을 정렬해야 할 텐데, 여기서 위에 말한 재귀 방법을 사용하는 것이다.

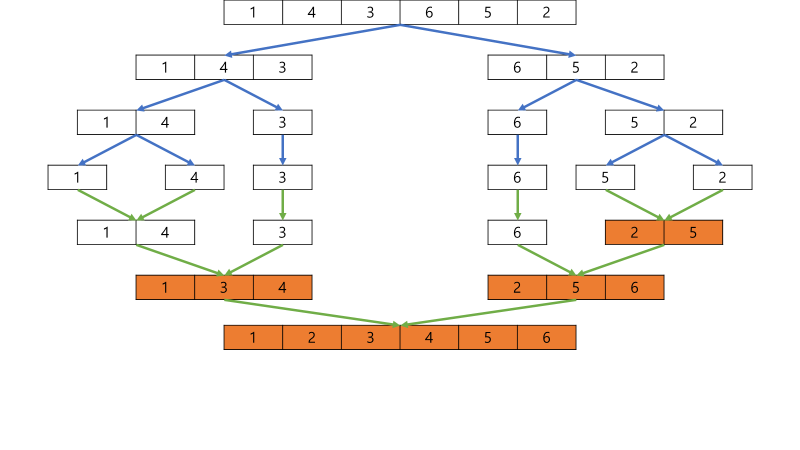
재귀가 무엇인가는 아래와 같다.

일단 나눈 배열을 더 이상 나눠지지 않을 때까지 나누기를 반복한다.

이제 이렇게 가장 잘게 나눈 배열(빨간색)들은 정렬되어 있으므로(인덱스가 하나뿐이니까) 위 알고리듬으로 합치기를 반복한다.

이렇게 되면 최초로 나눈 두 배열이 정렬되었다. 이 둘을 위 알고리듬으로 합칠 수 있다!

코드로 구현

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76

#include <iostream>
#include <vector>

using namespace std;

// A는 원본배열, p는 시작 인덱스, q는 가운데, r은 끝
void merge(int A[],int p,int q,int r){
    int a = q-p+1; //나눈 왼쪽 원소개수
    int b = r-q; //나눈 오른쪽 원소개수
    
    
    // A를 왼쪽/오른쪽으로 나눠 저장할 배열 생성(아래 이유로 배열 개수+1)
    vector<int> left(a+1);
    vector<int> right(b+1);
    
    // A의 왼쪽부분을 left에
    for (int i=0;i<a;i++){
        left[i] = A[p+i];
    }
    // A의 오른쪽부분을 right에
    for (int i=0;i<b;i++){
        right[i] = A[q+i+1];
    }
    
    
    // 한쪽이 먼저 끝날경우 나머지 처리를 위해 양쪽의 끝을 무한대로
    left[a]=99999;
    right[b]=99999;
    
    // 양쪽 인덱스
    int i = 0;
    int j = 0;
    
    // 비교 과정
    for(int k=p;k<=r;k++){
        if (left[i]<=right[j]){
            A[k] = left[i];
            i++;
        }
        else{
            A[k] = right[j];
            j++;
        }
    }
}

// 재귀하는 곳 - p는 A의 시작인덱스, r는 끝인덱스
void mergesort(int A[],int p,int r){
    // 끝인덱스가 시작 인덱스보다 커야-재귀 조건-완전히 쪼개지면 실행하지 않기
    if (p<r){
        // 가운데 인덱스 q 생성
        int q = (p+r)/2;
        // A의 왼쪽을 재귀
        mergesort(A,p,q);
        // A의 오른쪽을 재귀
        mergesort(A,q+1,r);
        // 정렬
        merge(A,p,q,r);
    }
}

int main(){
    int n;
    cin>>n;
    int tosso[n];
    for(int i=0;i<n;i++){
        cin>>tosso[i];
    }
    cout<<sizeof(tosso)-1<<endl;
    mergesort(tosso,0,(sizeof(tosso)/sizeof(tosso[0]))-1);
    
    for(int i=0;i<n;i++){
        cout<<tosso[i]<<endl;
    }
    return 0;
}

우선 코드이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14

// 재귀하는 곳 - p는 A의 시작인덱스, r는 끝인덱스
void mergesort(int A[],int p,int r){
    // 끝인덱스가 시작 인덱스보다 커야-재귀 조건-완전히 쪼개지면 실행하지 않기
    if (p<r){
        // 가운데 인덱스 q 생성
        int q = (p+r)/2;
        // A의 왼쪽을 재귀
        mergesort(A,p,q);
        // A의 오른쪽을 재귀
        mergesort(A,q+1,r);
        // 정렬
        merge(A,p,q,r);
    }
}

여기에 주목해보자. merge() 함수는 위 알고리듬을 수행하는 함수이다. 그럼 mergesort()는?

(1,4,2,3,5,6)을 mergesort()에 넣으면…

  • 일단 p는 0, r은 5가 될 테이다. p<r에 만족한다.
  • q는 (5+0)/2 = 2.5=>2 즉 가운데 인덱스이다.
  • 이제 mergesort(0,2)/mergesort(3,5)를 먼저 수행한다.
  • mergesort(0,2)는 다시 mergesort(0,1)/mergesort(2,2), merge(0,1,2)로 나뉘어진다.
    • mergesort(0,1)은 mergesort(0,0)/mergesort(1,1) 로 나뉘어질 텐데, 이 둘은 p<r 조건에 맞지 않으므로 그냥 넘어가진다.
      • 즉 mergesort(0,1)은 결국 merge(0,0,1)만 수행된다.
    • mergesort(2,2)도 마찬가지로 그냥 넘어간다.
    • 따라서 mergesort(0,2)는 merge(0,0,1)→merge(0,1,2) 이 순으로 수행된다.
  • mergesort(3,5)는 다시 mergesort(3,4)/mergesort(5,5) 및 merge(3,4,5)로 나뉘어진다.
    • mergesort(3,4)는 mergesort(3,3)/(4,4)로 나뉘어지고, 마찬가지 이유로 merge(3,3,4) 만 수행된다.
    • mergesort(5,5)는 수행되지 않는다.
    • 따라서 mergesort(3,5)는 merge(3,3,4)→merge(3,4,5) 순으로 수행된다.
  • 최종적으로 mergesort(0,5)는 merge(0,0,1)→merge(0,1,2)→merge(3,3,4)→merge(3,4,5)→merge(0,2,5) 이렇게 실행되는 것이다.

힙 정렬

계속…

알고리듬
algorithm sort
This post is licensed under CC BY 4.0 by the author.