알고리듬 문제를 풀어보자-bfs
bfs 알고리듬
예전에 dfs 알고리듬 문제를 다룬 적이 있었다.
이번에는 dfs의 단짝인 bfs 알고리듬 문제를 연구해보자..
bfs란
bfs 알고리듬은 그래프 완전탐색에 사용되는 알고리듬으로 dfs와 달리 그래프의 너비를 우선으로 삼는다.
그래프가 뭐고, 그래프 (완전)탐색이 무엇인지는 위 링크에서
너비가 우선이라는 말은, 그림을 그려서 보는게 더 편하다.

이런 그래프가 있다고 치자.
dfs는 지난 시간에 이렇게 찾는다고 했다.
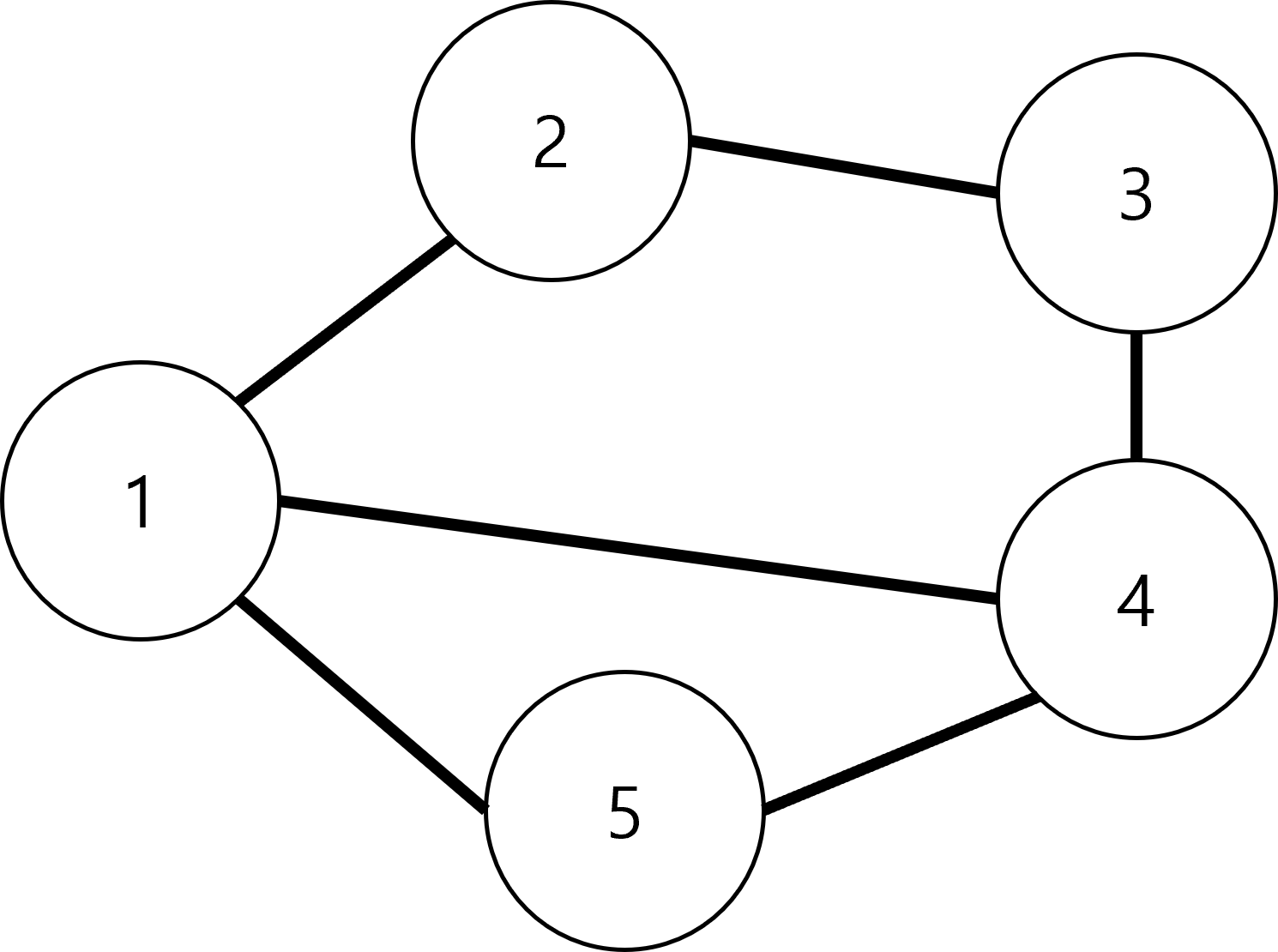
시작 노드를 정하고 연결된 노드들을 쭉 따라가며 탐색한 뒤1
연결된 노드가 없거나 전부 탐색한 노드들이면 다음 연결된 노드로 시작해 계속 반복하는 방식이다.
bfs는 그 반대이다.
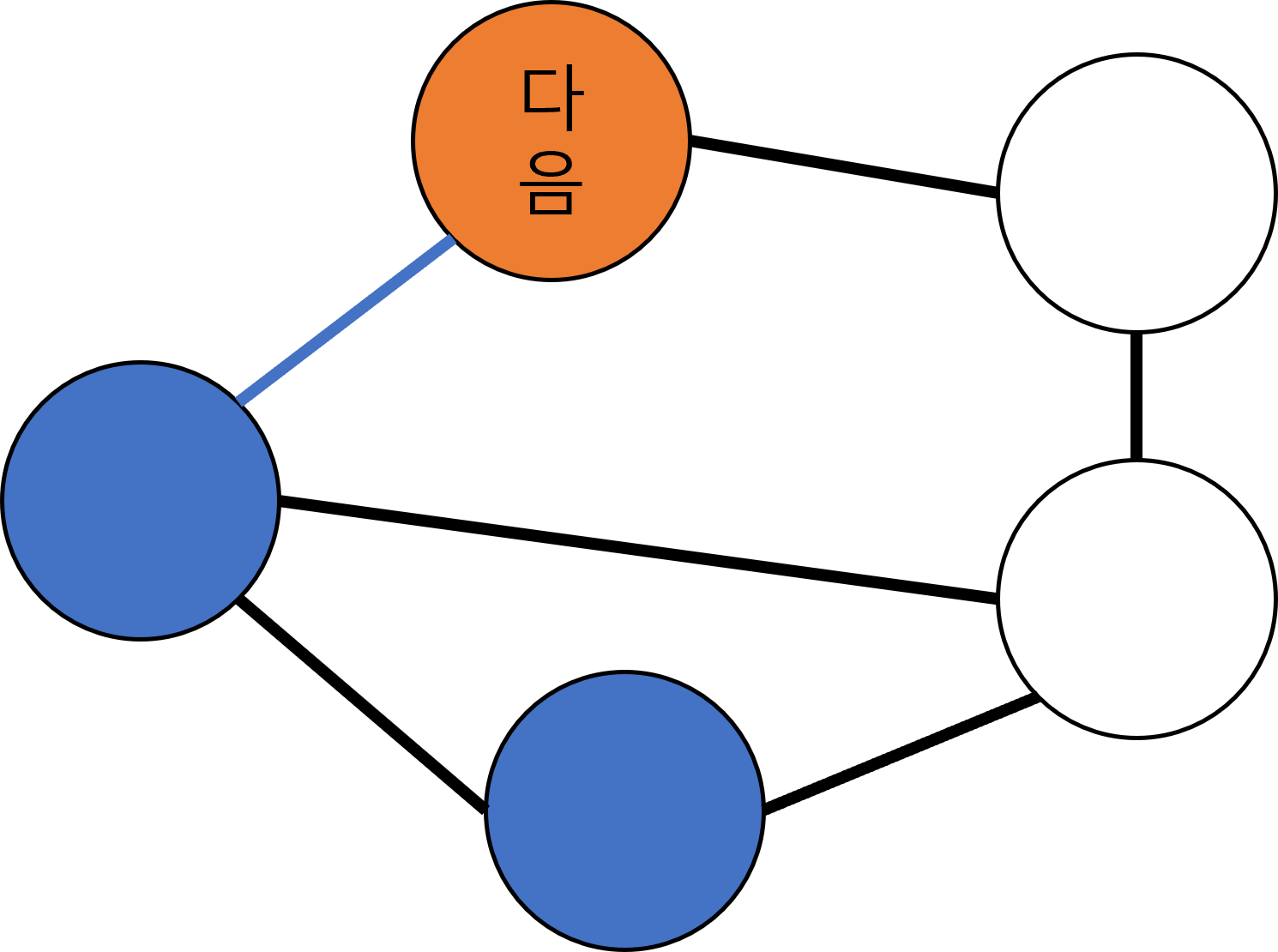
아래 그림에서 주황색은 탐색할 기준 노드, 파란색은 탐색된 노드이다.
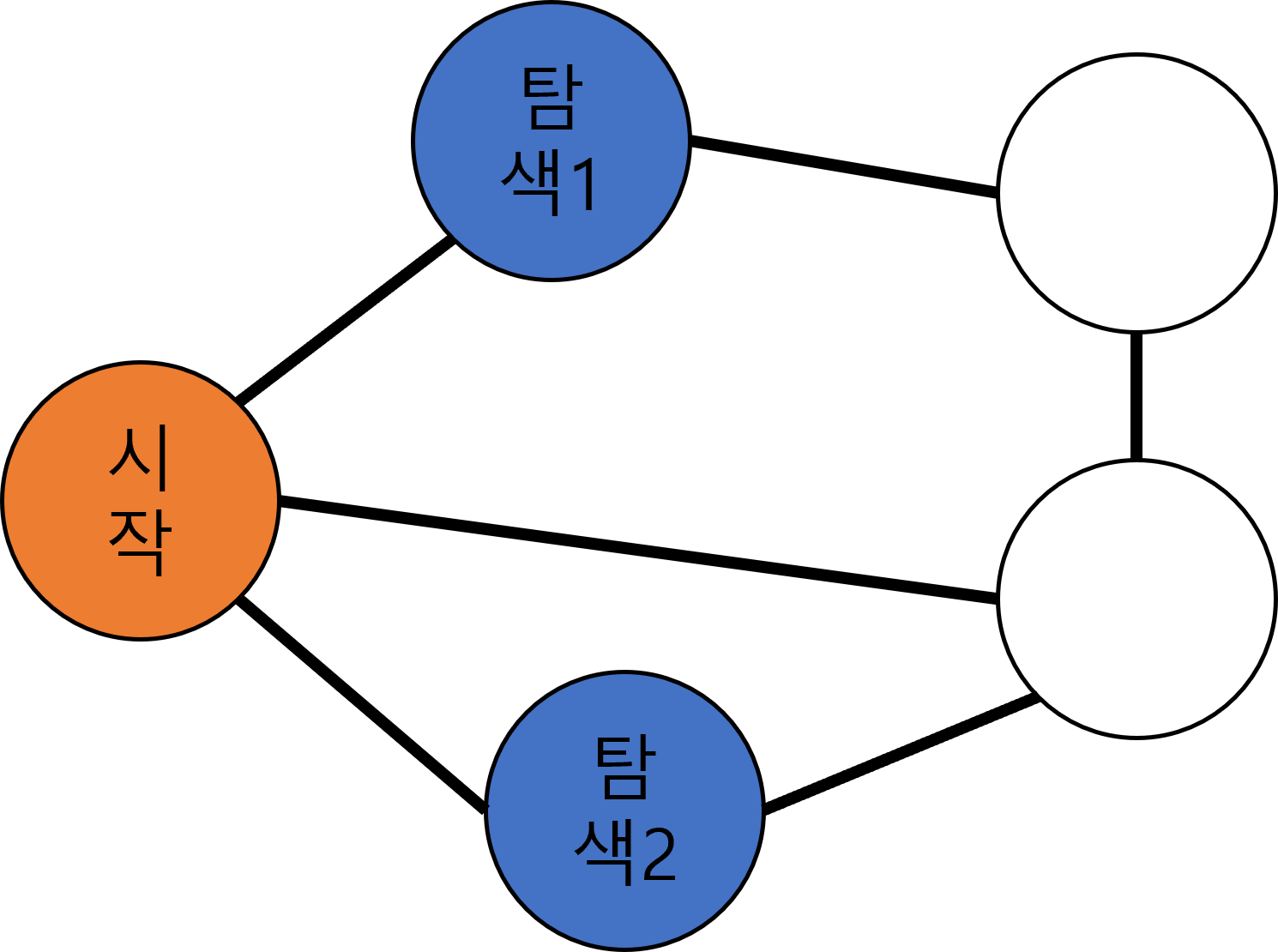
먼저 시작 노드를 기준으로 잡고 연결된 노드들을 먼저 탐색한다. 탐색 순서는 가나다 순서처럼 알아서 정하면 된다.
중요한 점은, 탐색한 노드를 기준 목록에 순서대로 집어넣어야 한다. 즉 여기서는 12시 노드->6시 노드 순으로 기준 목록에 들어간다.
기준 목록-12시, 6시
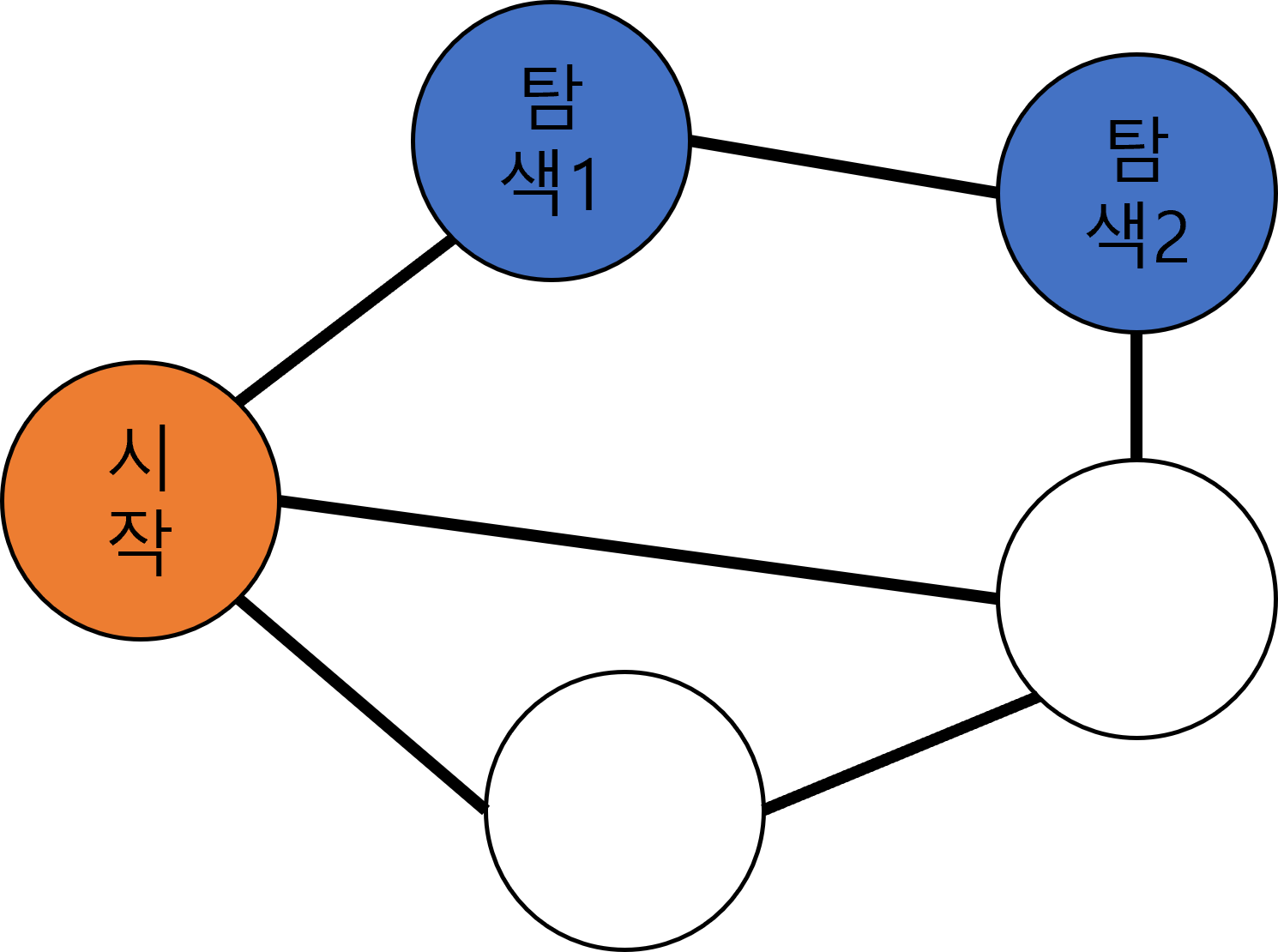
(dfs와의 차이-dfs는 위 그림처럼 노드를 계속 연결해 나아간다.)
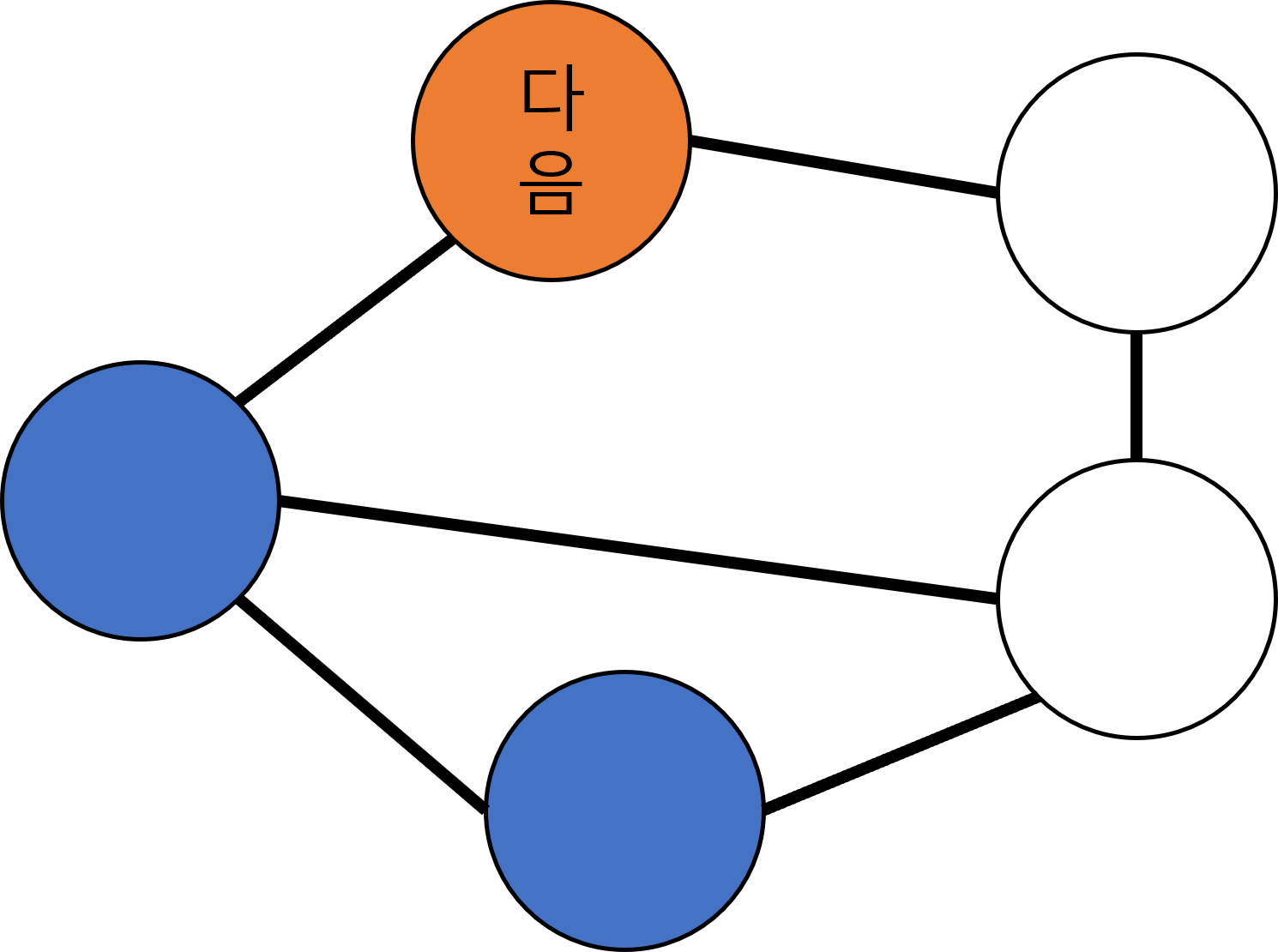
탐색이 끝나면, 이제 기준 목록에 있는 맨 앞의 노드를 빼내어 기준 노드로 삼는다.
기준 목록-(12시 빠짐) 6시
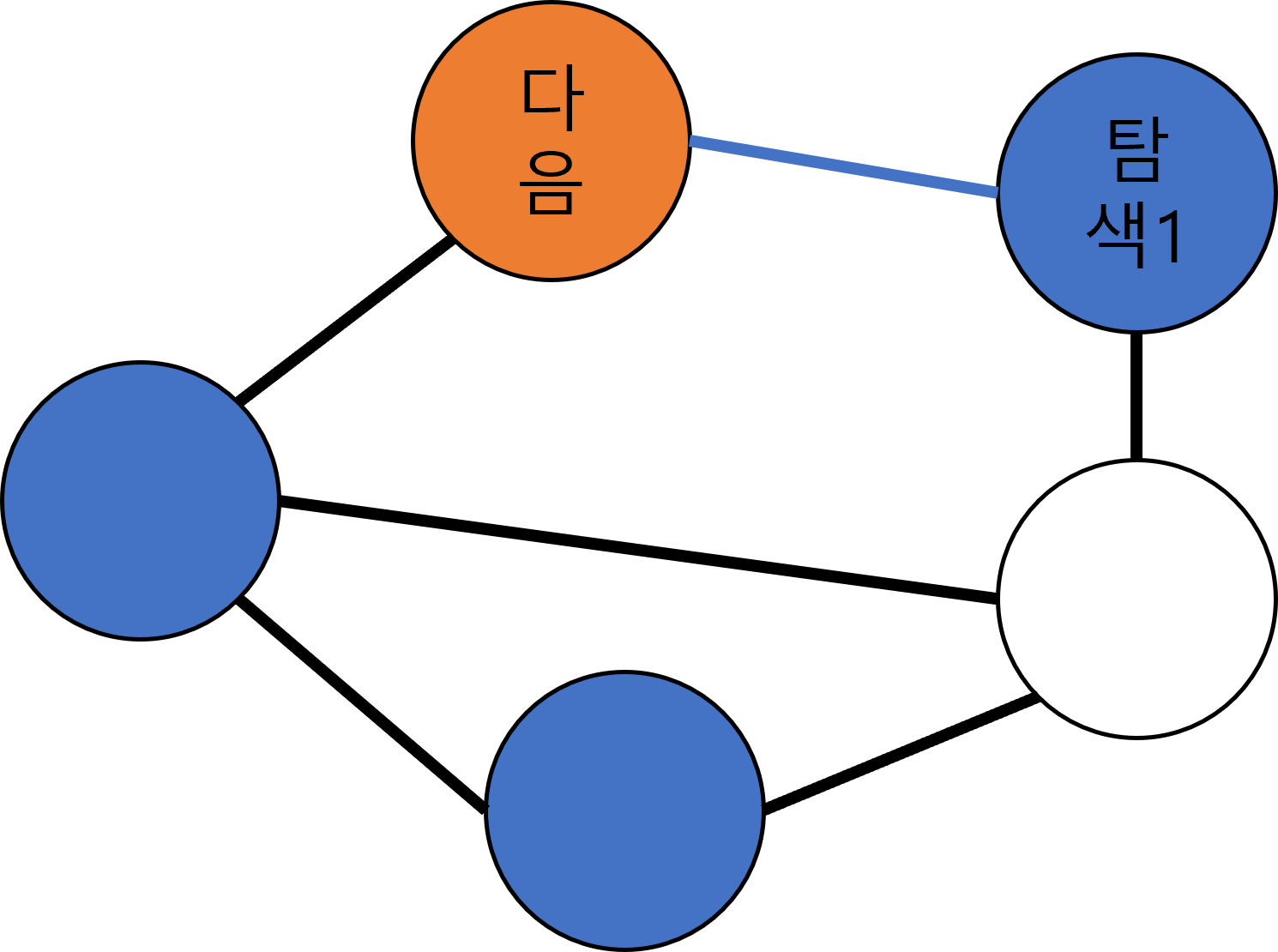
이제 변경된 기준 노드와 연결된 노드를 찾는다. 이미 탐색한 노드라면 제외한다.
마찬가지로 탐색한 노드는 기준 목록에 넣는다.
기준 목록-6시,1시
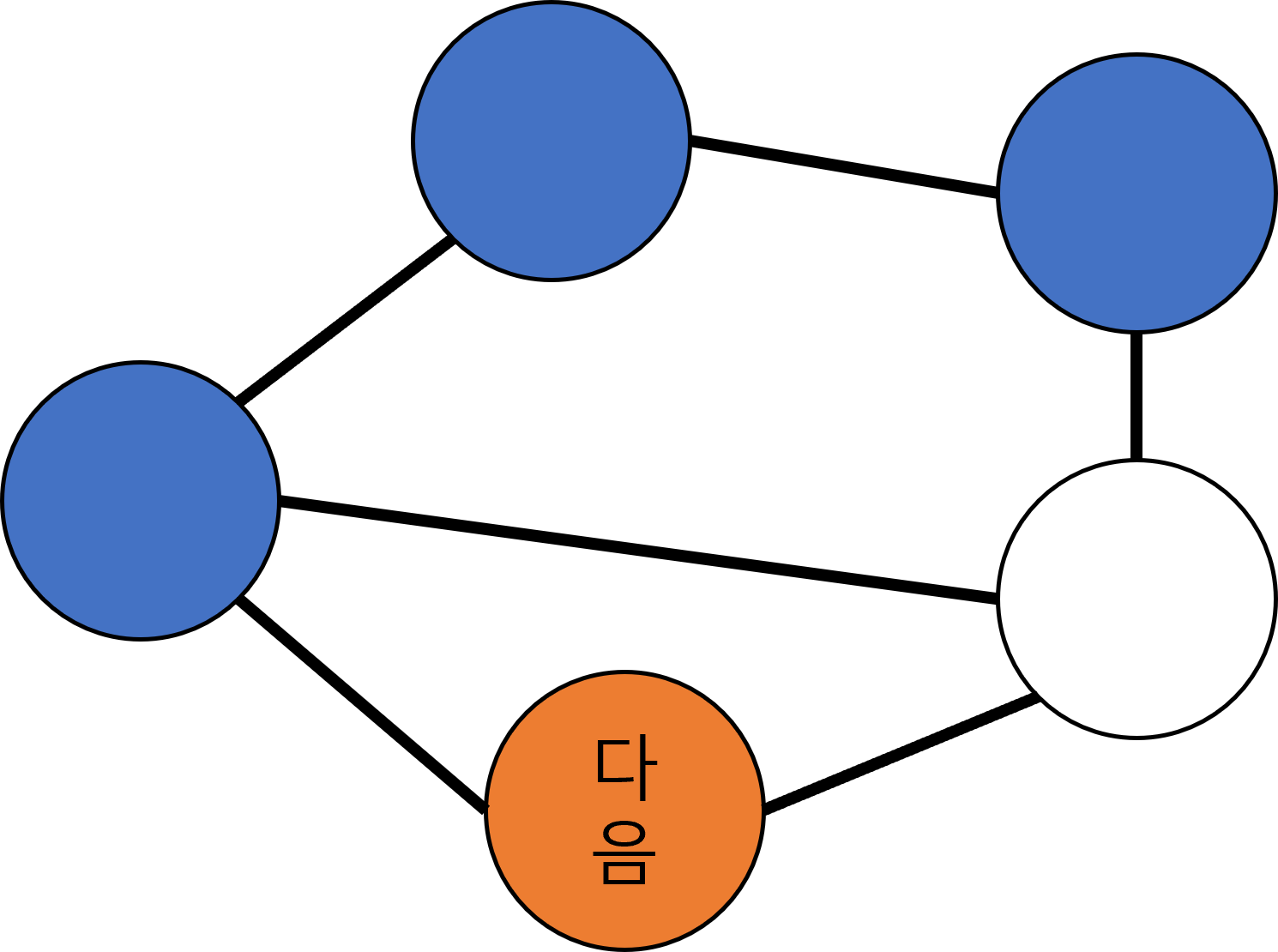
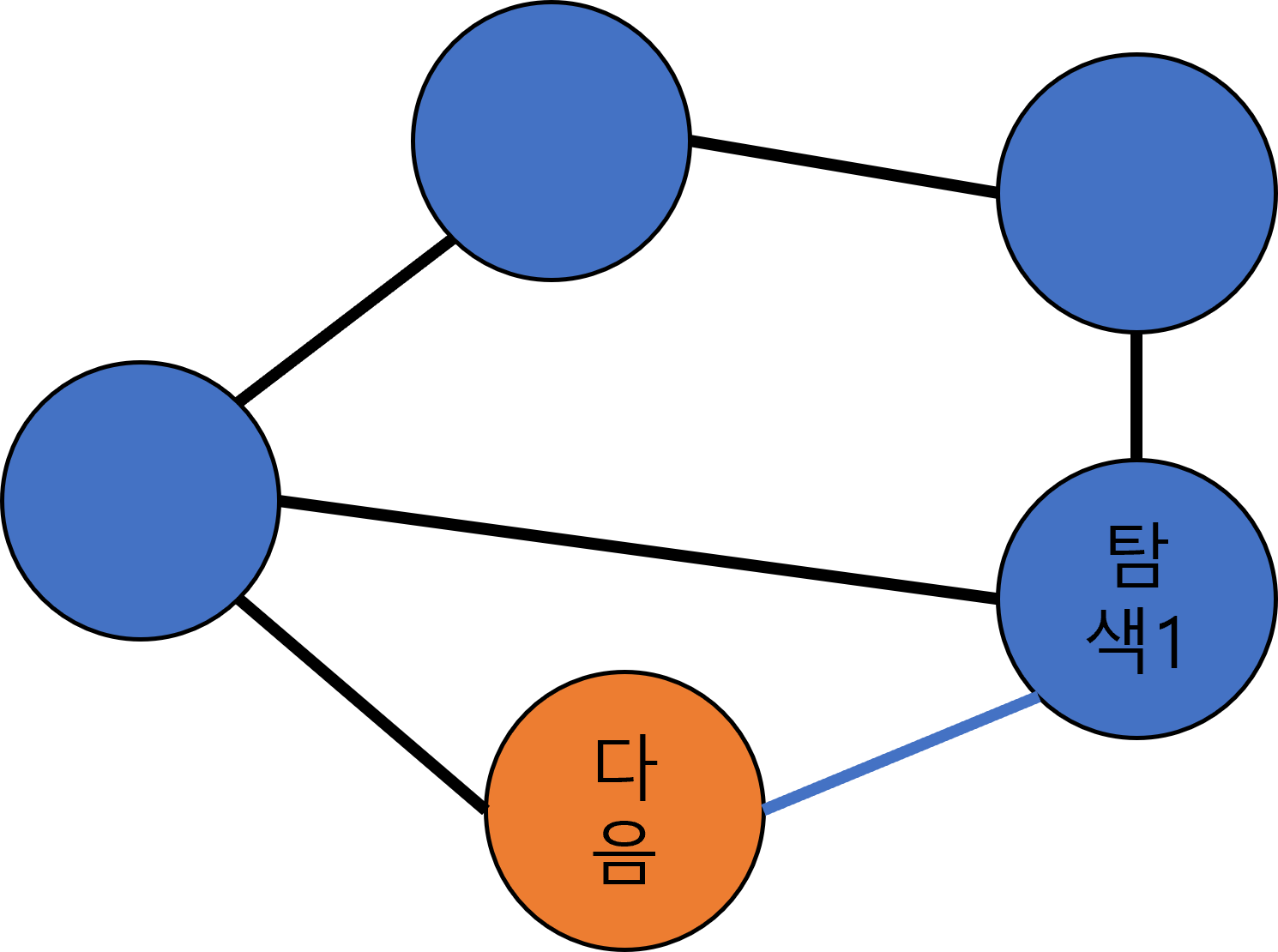
마찬가지로 끝나면 기준 노드를 목록에서 빼내어 정하고, 반복한다.
기준 목록-(6시 빠짐) 1시,5시
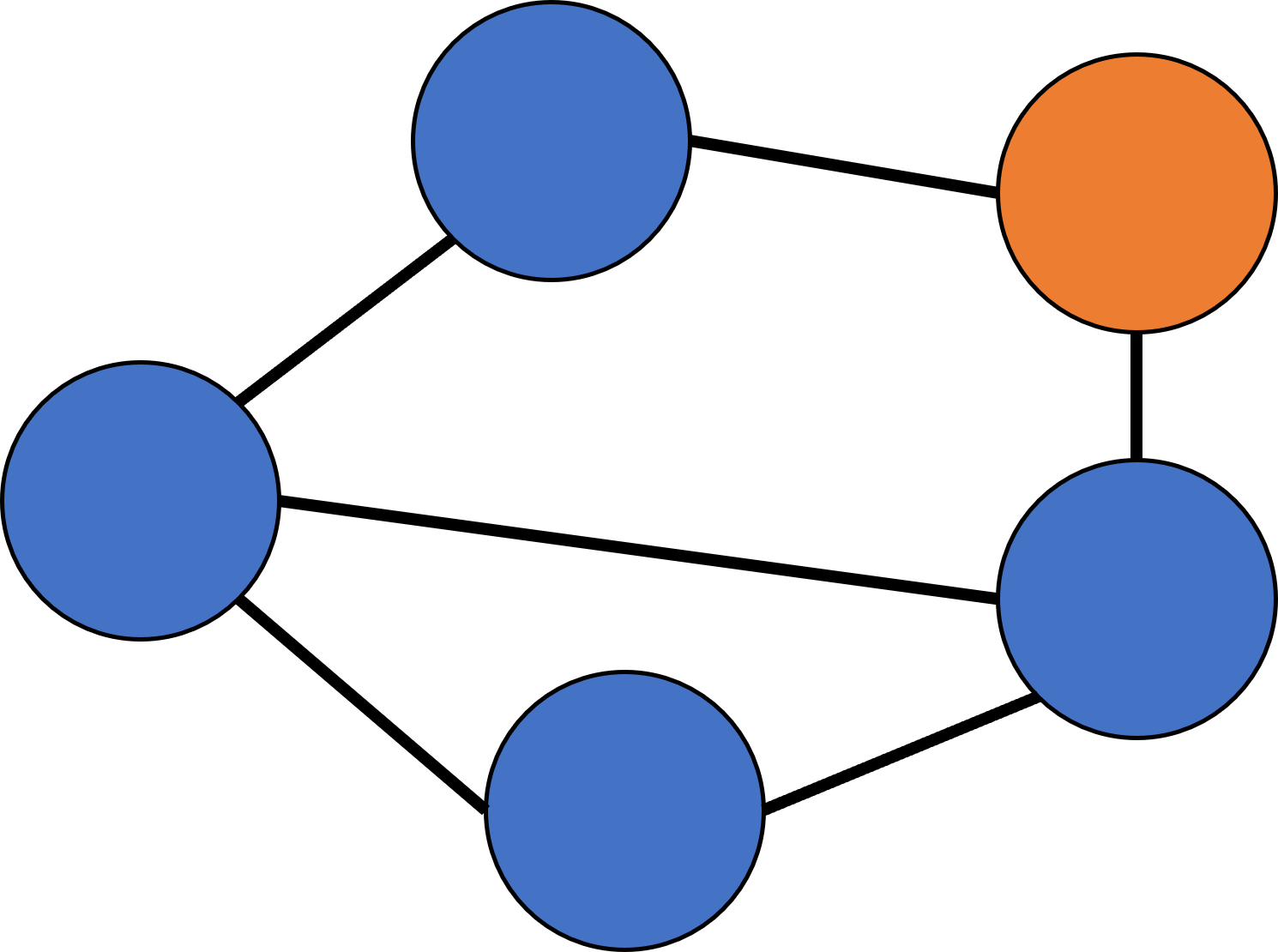
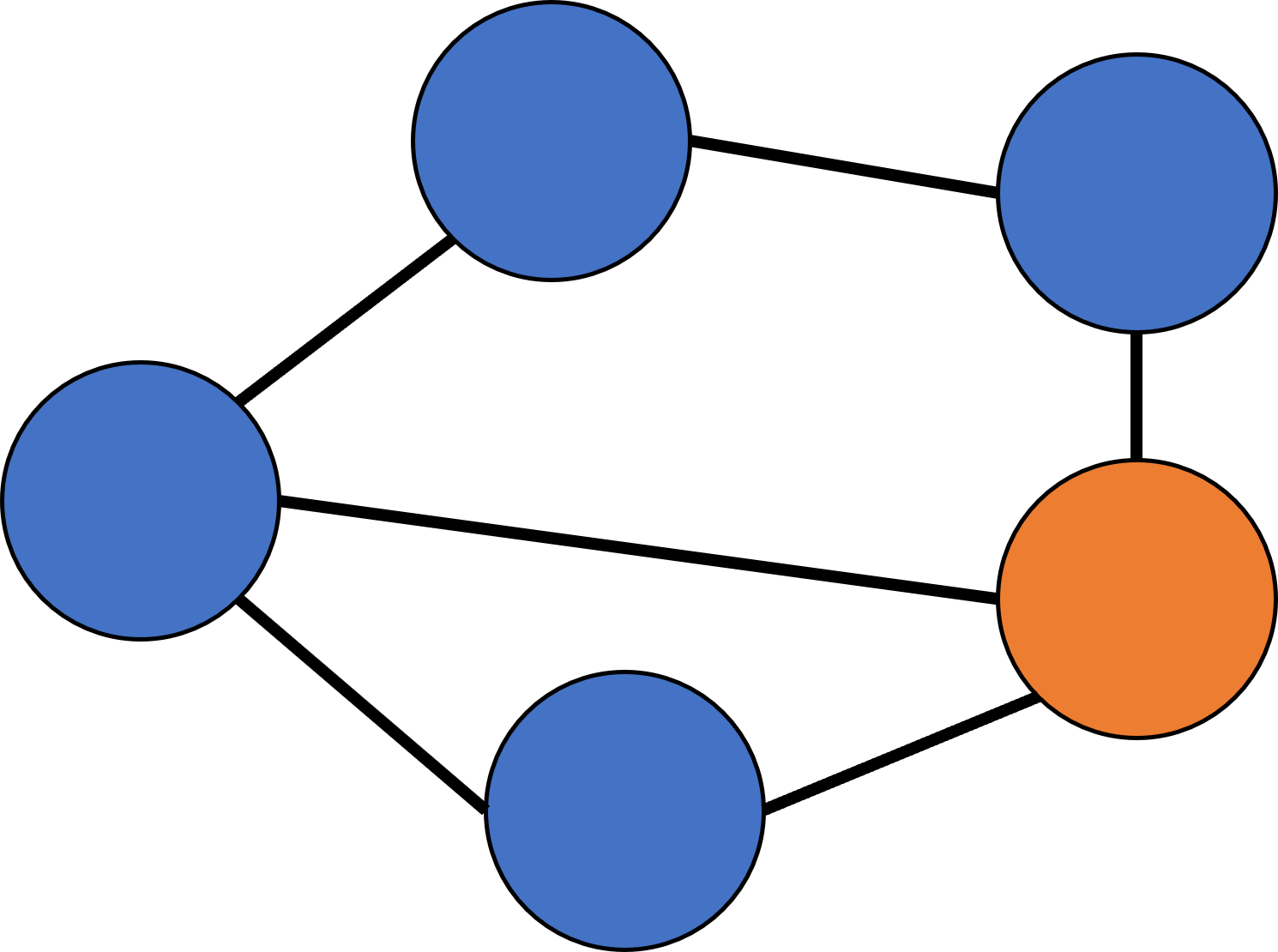
기준 목록에 1시와 5시 노드가 남지만, 이 둘과 연결된 노드는 모두 탐색한 노드이다. 따라서 탐색 끝!
코드로 구현하기
기준 목록에서 눈치채었을수도 있지만, 스택 자료구조를 사용하면 매우 편하게 구현할 수 있다.
스택 자료구조는 순서가 있는 리스트의 일종인데, 자료가 들어가면 맨 뒤에 넣고, 자료를 뺄 때는 맨 앞의 것을 빼는2 원칙을 지켜야 한다.
기존 언어의 리스트로 구현하려면 꽤 머리를 써야겠지만, 다행히 요즘 프로그래밍 언어에서는 이 구조를 일종의 자료형으로 지원하여 넣고 뺄때 알아서 위처럼 해준다.
간단한 실전문제를 직관적으로 알기 위해 파이썬으로 구현해보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
문제
그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.
입력
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.
출력
첫째 줄에 DFS를 수행한 결과를, 그 다음 줄에는 BFS를 수행한 결과를 출력한다. V부터 방문된 점을 순서대로 출력하면 된다.
예제 입력 1
4 5 1
1 2
1 3
1 4
2 4
3 4
예제 출력 1
1 2 4 3
1 2 3 4
여기서는 DFS도 구현하라 했으니, 추억을 살려 DFS도 한번 만들어보자.
명심할 점은, DFS는 재귀, BFS는 스택을 사용하면 편하게 풀 수 있다는 점이다. 원리야 이 사이트에서 다 설명해주었으니 넘어가고.
1
2
3
4
5
6
7
8
9
10
node, edge, start = map(int,input().split())
graph = [[] for i in range(node)]
visited = [0 for i in range(node)]
for i in range(edge):
begin, end = map(int,input().split())
graph[begin-1].append(end)
graph[end-1].append(begin)
# 작은 것부터 방문하라 했으니까 오름차순 정렬
for i in graph:
i.sort()
우선 입력을 받아 각 노드당 인접 여부를 나타내는 2중배열(graph)과 방문 여부를 나타내는 1차원 배열(visited)을 나타낸다. 이 과정은 DFS 문서에도 있으니 생략.
일단 BFS부터 구현해본다.
1
2
3
4
5
6
7
8
9
10
def bfs(graph,visited,start):
visited[start-1] = 1
kijun = [start]
while kijun:
injop = kijun.pop(0)
print(injop, end=' ')
for i in range(0,len(graph[injop-1])):
if visited[graph[injop-1][i]-1] == 0:
kijun.append(graph[injop-1][i])
visited[graph[injop-1][i]-1] = 1
일단 시작 노드(start)는 방문했으니 체크해준다(visited[start-1] = 1)
그리고 기준 목록에 해당하는 스택(kijun)을 하나 만들고 시작 노드를 넣어준다.
이제 기준 목록이 빌 때까지 아래를 반복한다.
- 기준 목록에서 맨 앞의 것을 뺀다.(
injop = kijun.pop(0)) 이 뺀 것은 이제 기준 노드가 된다.(injop) - 출력해주는 것도 잊지 말고
- 여기서부터 중요한데,
graph[injop-1]은 injop, 즉 기준 노드의 인접힌 노드가 있는 배열이다. - 따라서 이 배열을 돌면서 그 속의 노드들이 방문하지 않았다면(
visited[graph[injop-1][i]-1] == 0) - 기준 목록에 추가해주고(
kijun.append(graph[injop-1][i])) - 방문 여부도 1로 만들어준다.(
visited[graph[injop-1][i]-1] = 1)
참고로 노드 번호는 graph, visited 관계없이 배열 인덱스보다 1이 많으니 꼭 인덱싱 할때 1을 빼주자.
그 다음 DFS도 구현해본다. 이것도 DFS 문서에 있으니 설명 생략
1
2
3
4
5
6
def dfs(graph,visited,start):
visited[start-1] = 1
print(start, end=' ')
for i in range(len(graph[start-1])):
if visited[graph[start-1][i]-1] == 0:
dfs(graph,visited,graph[start-1][i])
따라서 전체 코드는
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
node, edge, start = map(int,input().split())
graph = [[] for i in range(node)]
visited = [0 for i in range(node)]
def dfs(graph,visited,start):
visited[start-1] = 1
print(start, end=' ')
for i in range(len(graph[start-1])):
if visited[graph[start-1][i]-1] == 0:
dfs(graph,visited,graph[start-1][i])
def bfs(graph,visited,start):
visited[start-1] = 1
kijun = [start]
while kijun:
injop = kijun.pop(0)
print(injop, end=' ')
for i in range(0,len(graph[injop-1])):
if visited[graph[injop-1][i]-1] == 0:
kijun.append(graph[injop-1][i])
visited[graph[injop-1][i]-1] = 1
# 입력값
for i in range(edge):
begin, end = map(int,input().split())
graph[begin-1].append(end)
graph[end-1].append(begin)
for i in graph:
i.sort()
# dfs 개시
dfs(graph,visited,start)
# 한줄 띄어주기
print()
# visited 초기화
visited = [0 for i in range(node)]
# bfs 개시
bfs(graph,visited,start)