Post

알고리듬 문제를 풀어보자-이상한 문제

Posted Updated
By Kaebal Kim
9 min read
알고리듬 문제를 풀어보자-이상한 문제

이상한 문제

5월 들어 코딩테스트 준비에 열심이기 때문에 계속 프로그래머스(programmers.co.kr)/acmicpc(acmicpc.net) 등을 전전하며 문제를 풀고 있다.

그러다 쉬울 것 같으나 의외로 힘들고, 풀이를 보니 허를 찌르는 문제들을 발견했는데, 이들을 소개해보자 한다.

멀쩡한 사각형

(문제 내용)[https://programmers.co.kr/learn/courses/30/lessons/62048]

algo3-img1

정~말 쉬워 보이나 은근히 마주하면 어떻게 풀 지 모른다. 이유는 푸는 방법이 거창한 dfs니/탐욕이니/동적 계산 등이 아니기 때문이다.

본인도 처음에는 전체를 조그많게 나눠 푸는 동적 프로그래밍인 줄 알았지만, 현실은 훨~씬 간단했다.

풀이 방법

가능한 경우를 많이 그려봐 규칙을 찾는 것이 중요하다.

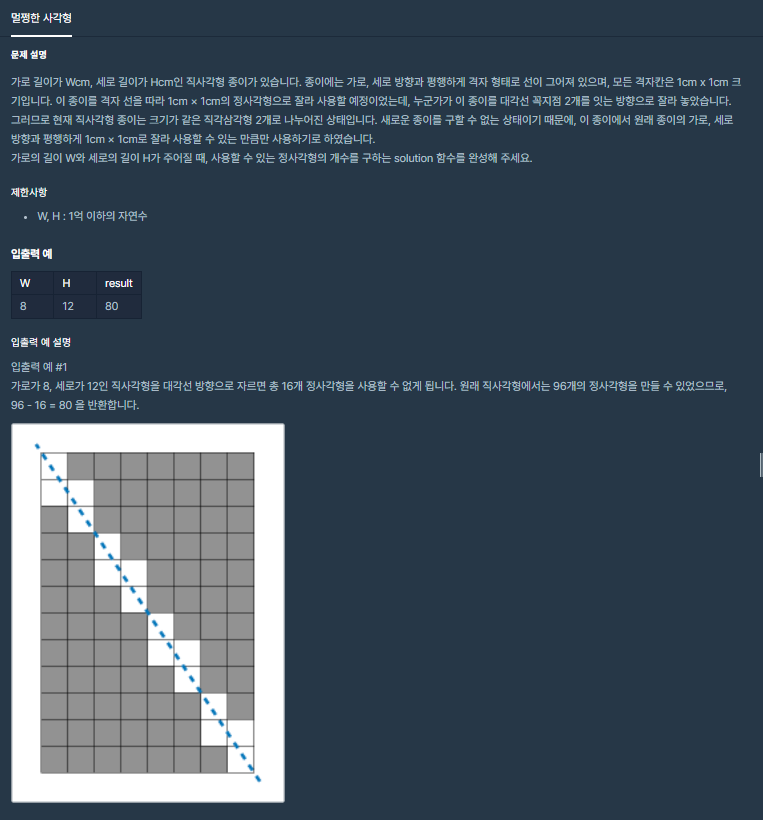
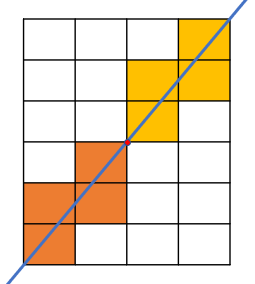
일단 위 문제의 그림으로 생각해보면…

algo3-img2

어짜피 대각선을 어떻게 긋든 지나가는 사각형의 개수는 같으므로 이렇게 생각해볼 수 있다.

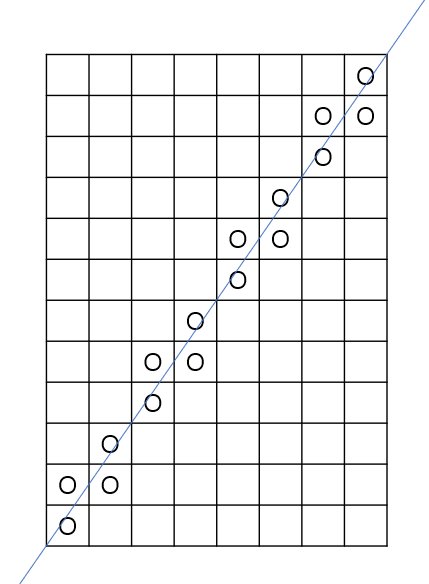
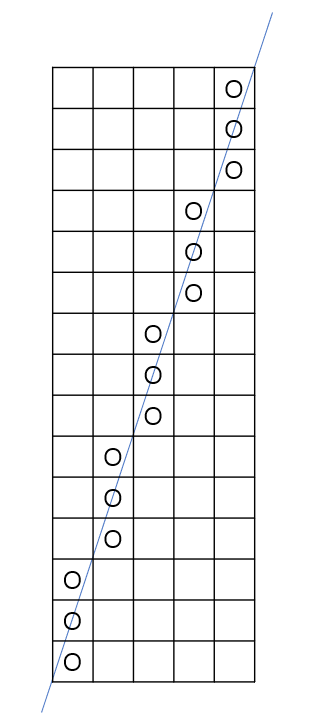
algo3-img3

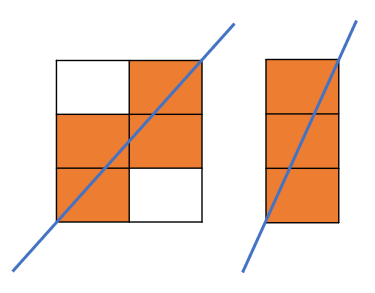
5x15인 사각형을 그려보면 이렇게 된다.

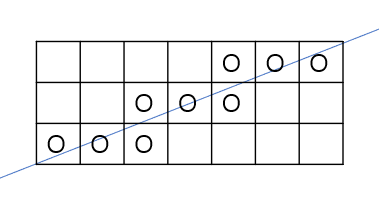
algo3-img4

7x3인 사각형은 이러네?

여기서 주목해보면, 7x3은 직선이 중간에 점을 거치지 않는데, 첫번째거(8x12)와 5x15는 직선이 작은 사각형의 곡지점을 지난다.
그리고 각 곡지점 단위로 지나가는 사각형들을 나눠보면, 하나의 무늬를 형성한다.
이게 무슨 말이냐면,

algo3-img5

이 4x6을 잘 보면, 직선이 가운데 곡지점을 지나가고, 그 점 양옆으로 지나가는 사각형들을 맞춰보면 테트리스 블록 무늬로 동일하다!

즉 직선이 곡지점을 지나는 경우에는 무늬의 개수, 무늬당 사각형 개수만 알면 정답이 나온다는 말이다.
그럼 이 둘은 어떻게 구하냐? 이건 수학적 능지가 있어야 알아챌 수 있다.

위 그림들을 잘 보면 8x12는 무늬의 개수가 4개,
5x15는 무늬의 개수가 5개, 7x3은 안지나가므로 제외, 4x6은 2개

눈치챘겠지만, 무늬의 개수는 바로 최대공약수다. 가로와 세로의 최대공약수.

이제 무늬당 사각형 개수만 알면 된다. 이건 다소 힘들텐데, 이것도 노다가로 알 수 있다. 아까 8x12와 5x15 각 무늬의 양 끝단을 기준으로 사각형을 잘라 보면

algo3-img6

이렇게 되는데… 이렇게 경우들을 계속 만들어 노가다 해보면 가로/최대공약수+세로/최대공약수-1이 지나가는 사각형 개수라는 경우에 수렴하게 된다. (가로세로/최대공약수)인 것은 잘린 사각형의 가로세로 길이가 전체 가로세로를 최대공약수로 나눈 것이기 때문

따라서 (가로/최대공약수+세로/최대공약수-1)*최대공약수 가 사각형 개수가 된다는 것이다.

실제로 계산해보면… 8x12에서 (8/4+12/4-1)x4 = 16, 5x15에서 (5/5+15/5-1)x5 = 15이 되는데, 위 그림에서와 일치한다!

그러면 이건 됐고, 이제 곡지점 안 지날때는 어떻게 하냐?
이것도 노가다이다. 계속해 보면 가로+세로-1이 지나가는 사각형 개수인 것을 알 수 있다.

따라서 정답은

1
2
3
4
5
6
7
8
9
10
11

import math

def solution(w,h):
    answer = 1
    t = w*h
    m = math.gcd(w,h)
    if m==1:
        answer = t-(w+h-1)
    else:
        answer = t-((w/m+h/m-1)*m)
    return answer

경우를 직접 만들어봐 수학적 규칙을 찾아야 한다는 점에서 코딩테스트 보다는 경진대회 에 어울리는 문제라고 생각한다.

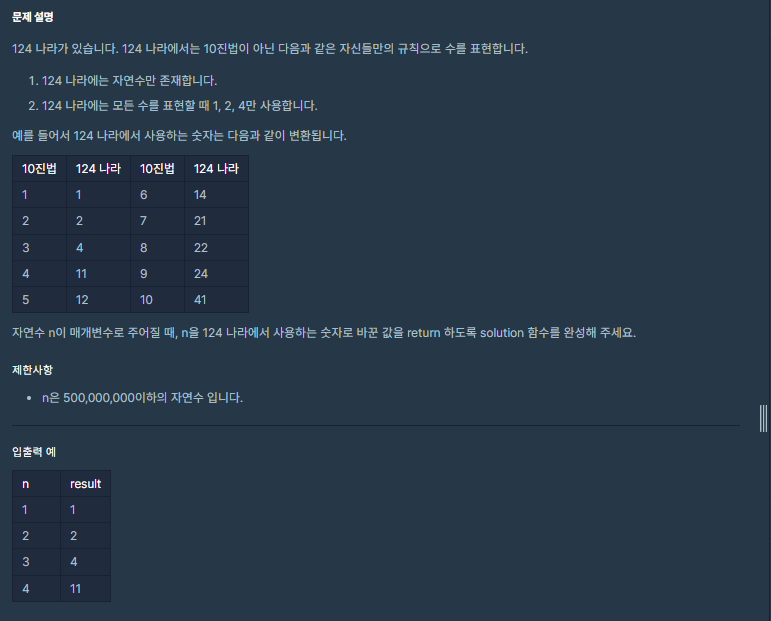
124 나라

문제 내용

algo3-img7

굉장히 귀찮은 문제이다. 일단 눈치 빠른 사람은 알겠지만 삼진법을 응용하면 된다. 그야 1,2,4만 쓰니까!

다만 그냥 삼진법이면 아무나 다 풀겠지, 조금 많~이 꼬았다. 그래서 십진법,삼진법,124 나라를 대조해보면..

십진법삼진법124
111
222
3104
41111
51212
62014
72121
82222
910024
………
1211044
13101111
………
15120114
………

보면 알겠지만 124 마을에서 4가 들어간 것을 제외하면 3진법과 똑같다.

그럼 이 4가 들어간 것을 어떻게 해결할 것인가? 이것 때문에 매우 해메서 결국 해결법을 봤는데… 예상보다 매~우 간단했다.

124에서 4가 나오는 경우는 원본 수자가 3으로 나눠떨어지는 경우다.
4가 나오면 양쪽의 자리수가 맞지 않는 경우가 생겨버리므로, 3진법 변환으로 진행하되 자리수를 맞추기 위해 3으로 나누어떨어지면 그 몫에 1을 빼주고, **0을 4로 치환해주면 된다.

몫에 1을 빼주는 이유는, 4=3x1+1이기 때문이다. 예를 들어 볼 수 있다.

만약 6일 경우
6은 3진법으로 20, 124 나라로 14이다.
평소대로의 3진법 변환처럼 6을 3으로 나누면… 2/0으로 나누어떨어진다!
그러면 이 몫에서 1을 빼준다. 그러면 빼진 몫은 1이 될 테다. 이 몫을 또 3으로 나누면 0/1이 된다. 따라서 이런 식으로 변환된 3진법은 10이 될텐데, 여기의 0을 4로 치환해주면 14이 되어 정답이 되는 것이다.

마찬가지로 124 나라로 104가 나오는 15를 변환해보자. 15는 3으로 나누면 5/0일 텐데 나누어떨어지니까 5-1 해서 몫은 4 4를 3으로 나누면 1/1 1을 3으로 나누면 0/1 따라서 110->0을 4로변환->114 이렇게 되는 것이다.

즉 결론은…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

def solution(n):
    answer = ''
    samjinbop = ['4','1','2']
    tosso = []
    while n//3 != 0:
        a = n//3
        b = n%3
        if b==0:
            tosso.append(n%3)
            n -= 1
        else:
            tosso.append(n%3)
        n = n//3
    if n!=0:
        tosso.append(n)

    for i in range(len(tosso)-1,-1,-1):
        answer += samjinbop[tosso[i]]
    return answer

이 문제도 마찬가지로 고도의 수학적 사고력을 요구하는 경진대회에 알맞다고 생각한다…

알고리듬
algorithm greedy
This post is licensed under CC BY 4.0 by the author.