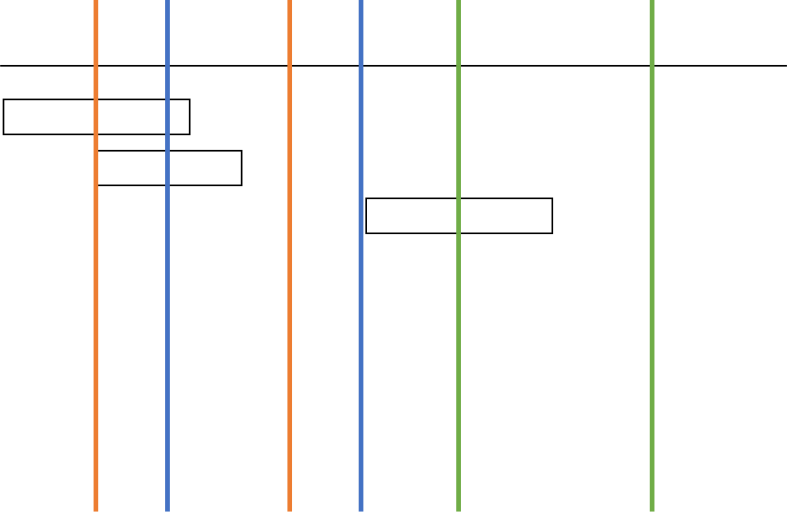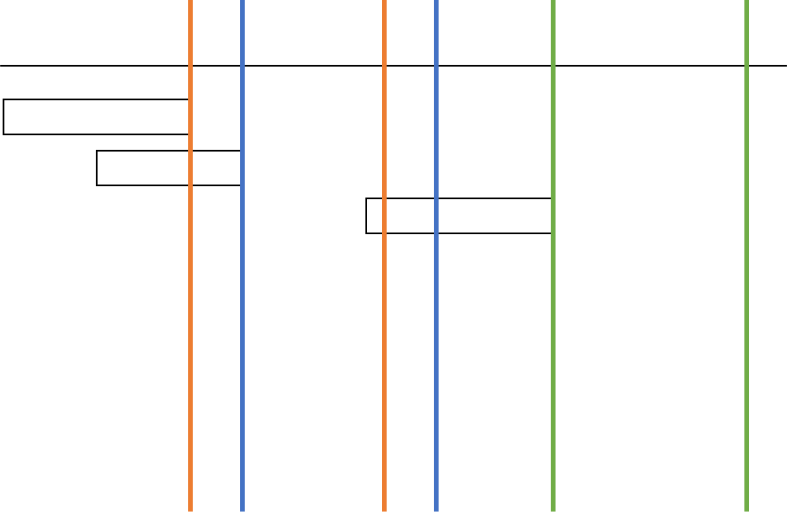알고리듬 문제를 풀어보자-탐욕

Posted May 18, 2022 Updated Apr 29, 2025

By Kaebal Kim

21 min read

알고리듬 문제를 풀어보자-탐욕

돌아온 알고리듬

구글 파이어베이스 프로젝트 글을 얼추 완성하여서 이제 다른 글을 쓸 수 있다!
그 첫 타자는 바로 알고리듬이다. 현재 기업에 이력서를 제출 중이라 적성검사를 대비하기 위해 매일 프로그래머스에 있는 기출문제를 한 문제씩 풀어보고 있는데, 어제 인상깊은 한 문제를 발견했기 때문이다.
한번 같이 풀어보자.

문제 내용

여기에서 볼 수 있다.

문제 설명
추석 트래픽
이번 추석에도 시스템 장애가 없는 명절을 보내고 싶은 어피치는 서버를 증설해야 할지 고민이다. 장애 대비용 서버 증설 여부를 결정하기 위해 작년 추석 기간인 9월 15일 로그 데이터를 분석한 후 초당 최대 처리량을 계산해보기로 했다. 초당 최대 처리량은 요청의 응답 완료 여부에 관계없이 임의 시간부터 1초(=1,000밀리초)간 처리하는 요청의 최대 개수를 의미한다.

입력 형식
solution 함수에 전달되는 lines 배열은 N(1 ≦ N ≦ 2,000)개의 로그 문자열로 되어 있으며, 각 로그 문자열마다 요청에 대한 응답완료시간 S와 처리시간 T가 공백으로 구분되어 있다.
응답완료시간 S는 작년 추석인 2016년 9월 15일만 포함하여 고정 길이 2016-09-15 hh:mm:ss.sss 형식으로 되어 있다.
처리시간 T는 0.1s, 0.312s, 2s 와 같이 최대 소수점 셋째 자리까지 기록하며 뒤에는 초 단위를 의미하는 s로 끝난다.
예를 들어, 로그 문자열 2016-09-15 03:10:33.020 0.011s은 "2016년 9월 15일 오전 3시 10분 33.010초"부터 "2016년 9월 15일 오전 3시 10분 33.020초"까지 "0.011초" 동안 처리된 요청을 의미한다. (처리시간은 시작시간과 끝시간을 포함)
서버에는 타임아웃이 3초로 적용되어 있기 때문에 처리시간은 0.001 ≦ T ≦ 3.000이다.
lines 배열은 응답완료시간 S를 기준으로 오름차순 정렬되어 있다.
출력 형식
solution 함수에서는 로그 데이터 lines 배열에 대해 초당 최대 처리량을 리턴한다.
입출력 예제
예제1
입력: [
"2016-09-15 01:00:04.001 2.0s",
"2016-09-15 01:00:07.000 2s"
]

출력: 1

예제2
입력: [
"2016-09-15 01:00:04.002 2.0s",
"2016-09-15 01:00:07.000 2s"
]

출력: 2

설명: 처리시간은 시작시간과 끝시간을 포함하므로
첫 번째 로그는 01:00:02.003 ~ 01:00:04.002에서 2초 동안 처리되었으며,
두 번째 로그는 01:00:05.001 ~ 01:00:07.000에서 2초 동안 처리된다.
따라서, 첫 번째 로그가 끝나는 시점과 두 번째 로그가 시작하는 시점의 구간인 01:00:04.002 ~ 01:00:05.001 1초 동안 최대 2개가 된다.

예제3
입력: [
"2016-09-15 20:59:57.421 0.351s",
"2016-09-15 20:59:58.233 1.181s",
"2016-09-15 20:59:58.299 0.8s",
"2016-09-15 20:59:58.688 1.041s",
"2016-09-15 20:59:59.591 1.412s",
"2016-09-15 21:00:00.464 1.466s",
"2016-09-15 21:00:00.741 1.581s",
"2016-09-15 21:00:00.748 2.31s",
"2016-09-15 21:00:00.966 0.381s",
"2016-09-15 21:00:02.066 2.62s"
]

출력: 7

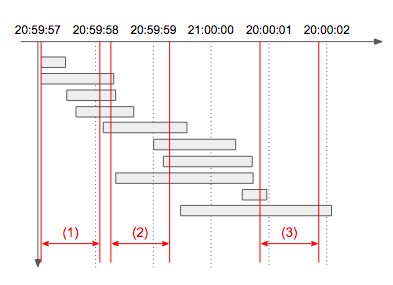
설명: 아래 타임라인 그림에서 빨간색으로 표시된 1초 각 구간의 처리량을 구해보면 (1)은 4개, (2)는 7개, (3)는 2개임을 알 수 있다. 따라서 초당 최대 처리량은 7이 되며, 동일한 최대 처리량을 갖는 1초 구간은 여러 개 존재할 수 있으므로 이 문제에서는 구간이 아닌 개수만 출력한다.

문제 설명

이 문제는 2017년 카카오톡 사 채용 예비고사 중 최상 난이도의 문제이다.
카카오톡 사 시험은 수능 수학문제마냥 문제 번호가 높아질수록 어려워지는데 초반 문제들은 노가다로도 풀 수 있으나(가끔씩 지문에 알고리듬을 주기도 한다) 후반으로 갈수록 dfs같은 고급 알고리듬을 알아야 풀 수 있는 문제가 주어진다.
이 문제도 후반 문제에 해당되는데, 글만 읽었을 때는 뭔 소리야 했으나 같이 주어진 그림(위 사진)을 보고 직감이 발동했다.

아! 탐욕(greedy) 알고리듬이다!

이 문제처럼 연속적인 값들을 주고 여기서 최대/최소값을 뽑아라 이러한 유형은 탐욕 알고리듬을 주로 사용한다.¹
그럼 그게 뭔데 ~~10ㄷ아~~ 이제 설명하겠다.

탐욕 알고리듬

탐욕 알고리듬은 사실 매우 애매한 개념이다. 위키백과의 말을 빌려 일단 설명하자면,

여러 경우 중 하나를 결정해야 할 때마다 그 순간 최선의 경우를 선택한다.

뭔 소리야?

쉽게 말하면 도박이다.
조금 더 간단히 설명하자면 선택의 상황에 놓였을 때, 현재 상황에서만 정답이라고 생각되는 것을 선택하여 이어나가는 방식으로, 그렇게 이어나간 최종 결과는 정답이 아닐 수도 있다. 때문에 이 알고리듬을 사용하려면 위 처럼 선택했을 때 최종 결과가 정답이라는 확신이 있어야 한다.²

이래도 납득하기 힘들 테니, 예시를 하나 보여주겠다.

길이가 10인 통나무가 있는데 이걸 4등분해야 돼요.
길이 1 단위로 자를 수 있어요. 자른 통나무는 길이별로 아래 가격에 팔 수 있어요.
1: 1원, 2: 2원, 3: 4원, 4: 8원, 5: 16원, ...
가장 돈을 많이 받게 잘라주세요.

이렇게 자를 수 있다는 말이다. 이런 식으로 4등분 했을 때 가장 많이 받기 위해서는?

4등분이므로 2/2/2/4, 2/2/3/3, … 이렇게 자를 수 있을 것이다.
길이가 길수록 2의 승으로 많이 팔 수 있으므로, 되도록이면 가장 길게 잘라야겠다.-최적의 선택
가장 긴 통나무가 나오는 1/1/1/7의 경우를 생각하면
가격: 1+1+1+64 = 67원
다른 선택을 볼 때, 2/2/2/4는 2+2+2+8=14원, 2/2/3/3은 2+2+4+4=12원, 3/3/3/1은 4+4+4+1=13원 등등 67원에 한참 못미친다.
따라서 1/1/1/7이 정답!

위 경우는 선택의 기회가 한번 밖에 없지만, 만약 파는 값이 달라져서 1/1/1/7이 가장 많이 못 벌때는

가장 긴 값이 7일 때
- 1/1/1/7
가장 긴 값이 6일 때
- ?/?/?/6 - 나머지 길이(4) 중 3등분했을 때 가장 길게 자를 수 있는 길이는 2
- ?/?/2/6 - 그 다음 나머지 길이(2) 중 가장 길게 자를 수 있는 1
- ?/1/2/6 - 나머지 1
- 최종 1/1/2/6
5일 때 - 마찬가지로 계산
- ?/?/?/5
- ?/?/3/5
- ?/1/3/5
- 1/1/3/5
4일 때
- ?/?/?/4
- ?/?/4/4
- ?/1/4/4
- 1/1/4/4
3 이하는 최대길이에 해당되지 않으므로 제외

이렇게 각 최대길이별로 탐욕 알고리듬을 수행한 뒤 나온 값들을 비교해서 가장 높은 값이면 된다!
위 문제가 이렇게 푸는 것이다.

문제 풀이

시간 계산

문제를 풀기 전에, 시작시간 계산을 위해 전처리 작업이 필요하다.
입력값으로 받는 S,T를 타임스탬프³ 형태로 변환해주자.

  
def solution(lines):
    answer = 0
    sijak = [] # 시작시간이 담기는 배열
    kut = [] # 완료시간이 담기는 배열
    
    for i in lines:
        desert,S,T = i.split() # 년월일(desert) 값은 배제-다 같으니까
        
        timestamp = 0 # 응답완료 시간의 타임스탬프-초 단위
        temp = S.split(':') # 시간 S가 HH:MM:SS.f 형태니까 HH/MM/SS.f 로 나누기
        timestamp+=int(temp[0])*3600 # 시간-초단위니까 3600 곱해서 더하기
        timestamp+=int(temp[1])*60 # 분-초단위니까 60 곱해서 더하기
        temp2 = temp[2].split('.') # 초는 밀리초도 포함하니까 SS/f로 나누기
        timestamp+=int(temp2[0]) # 초 값은 그냥 더하기
        timestamp+=int(temp2[1])*0.001 # 밀리초 값은 0.001 곱해서 더하기
        
        temp3 = T.replace('s','').split('.') # 처리시간 T도 타임스탬프 변환을 위해
        timestamp2 = 0 # 처리시간의 타임스탬프(초 단위)
        for j in range(len(temp3)): # 소수점이 붙은것도 있고 안붙은것도 있으므로
            timestamp2+=int(temp3[j])*pow(0.001,j) # 소수점이 붙으면 0.001 곱해서 더해주기
        # 예시-2.004은 2*(0.001^0)+4*(0.001^1) 이런식으로
        
        sijak.append(timestamp-timestamp2+0.001) # 시작시간은 완료시간에서 처리시간을 뺀 다음 처리시간이 시작시간 및 끝시간을 포함하므로 0.001초를 더해준 값
        kut.append(timestamp) # 완료시간은 그냥 그대로 넣기

이렇게 했을 때 출력해보면

lines = [“2016-09-15 01:00:04.001 2.0s”, “2016-09-15 01:00:07.000 2s”]
일 때
sijak = [3602.0020000000004, 3605.001]
kut = [3604.001, 3607.0]

이렇게 나올 것이다.(0.0000…4는 파이썬 특유의 소수점연산 오차이므로 무시해도 좋다)

탐욕 알고리듬 개시

  
    for i in range(len(lines)): # 각 요청을 읽어들이면서(lines,sijak,kut의 인덱스는 동일)
        count = 0 # 초당 최대처리량
        kijun = kut[i] # 최대처리량 측정 기준시각은 해당 요청이 끝나는 시각-탐욕 알고리듬의 최선 선택
        for j in range(i,len(lines)): # 해당 요청 다음의 것들을 읽어들이면서
            if sijak[j]<kijun+1: # 각 요청의 시작시각이 기준시각으로부터 1초 내에 있을경우-즉 기준시간 내에 요청이 포함될 시
                count+=1 # 최대처리량 하나씩 더하기
        answer = max(answer,count) # answer(이전 count값)및 count(현재)를 비교하여 더 큰것을 answer값으로
        
    return answer

그 다음 타임스탬프로 변환된 시작/완료시간인 sijak 및 kut 값을 가지고 탐욕 알고리듬을 돌리면 된다.
여기서 하는 최선의 선택은 최대처리량 측정 시작을 요청 완료시각으로 하는 것인데, 왜 이렇게 하는지는 아래 그림으로 설명하겠다.

그림을 그려서 풀어보자면

문제에서 요청 완료시각은 오름차순 정렬되있다고 한다.
즉 해당 요청(i) 보다 일찍 끝나는 요청(j)은 없다.
따라서 측정 기준시각을 해당 요청(i)시간 내로 잡되, 기준이 완료시각에 가까워질수록 더 멀리 내다볼 수 있기 때문에 다른 요청들을 더 포함할 수 있어진다.

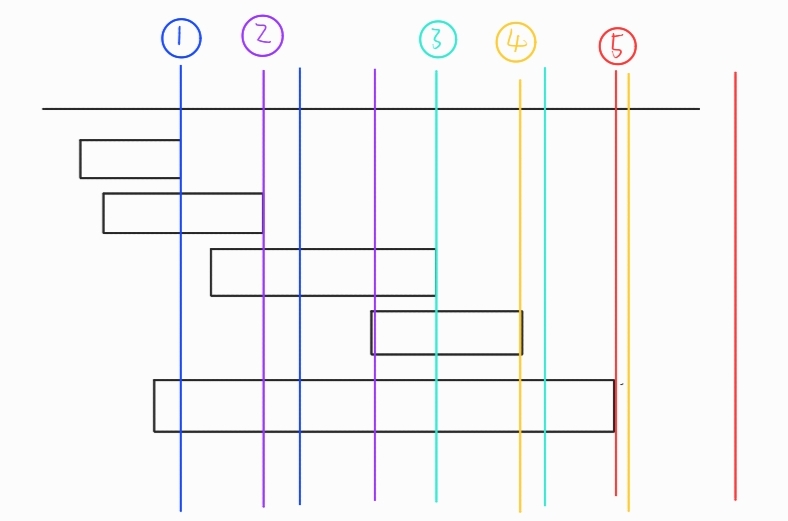
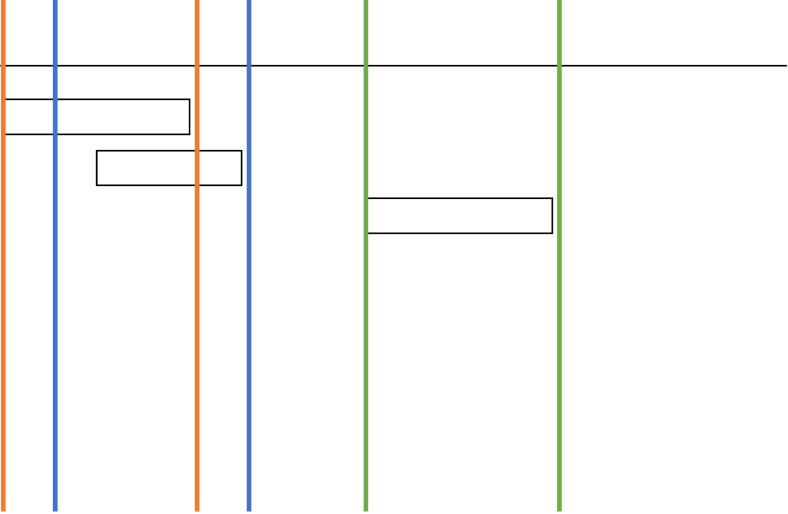
더 직관적으로 설명하기 위해, 아래 그림은 측정 기준시각을 순서대로 요청 시작, 요청 중간, 요청 완료 순으로 했을 때의 경우이다.

요청 시작(첫 번째 그림) 및 중간(두번째 그림)으로 기준을 잡았을 경우에는 첫번째 및 두 번째 기준(빨간색/파란색 선)이 마지막 요청을 포함하지 못하므로 최대 처리요청수는 2가 된다.
하지만 완료(세번째)로 잡으면 첫번째 기준(빨간색 선)이 마지막 요청을 포함해 최대 처리요청수가 3이 된다.

따라서 자신 요청을 포함하면서⁴, 가장 멀리 내다볼 수 있는 시각인 요청 완료시각으로 기준을 잡는 것이다.

참고로 위 코드에서 1초 내 포함을 판단할 때 <=가 아닌 <을 사용한 이유는
측정하는 1초도 결국은 시작시각과 끝시각을 포함하므로, 즉 0.000초부터 0.999초까지를 의미하는 것이므로
만약 <=을 사용하면 1.001초간 측정하는 것이 되어버리기 때문이다.

따라서 정답

  
def solution(lines):
    answer = 0
    sijak = [] # 시작시간이 담기는 배열
    kut = [] # 완료시간이 담기는 배열
    
    for i in lines:
        desert,S,T = i.split() # 년월일(desert) 값은 배제-다 같으니까
        
        timestamp = 0 # 응답완료 시간의 타임스탬프-초 단위
        temp = S.split(':') # 시간이 HH:MM:SS.f 형태니까 HH/MM/SS.f 로 나누기
        timestamp+=int(temp[0])*3600 # 시간-초단위니까 3600 곱해서 더하기
        timestamp+=int(temp[1])*60 # 분-초단위니까 60 곱해서 더하기
        temp2 = temp[2].split('.') # 초는 밀리초도 포함하니까 SS/f로 나누기
        timestamp+=int(temp2[0]) # 초 값은 그냥 더하기
        timestamp+=int(temp2[1])*0.001 # 밀리초 값은 0.001 곱해서 더하기
        
        temp3 = T.replace('s','').split('.') # 처리시간도 타임스탬프 변환을 위해
        timestamp2 = 0 # 처리시간의 타임스탬프(초 단위)
        for j in range(len(temp3)): # 소수점이 붙은것도 있고 안붙은것도 있으므로
            timestamp2+=int(temp3[j])*pow(0.001,j) # 소수점이 붙으면 0.001 곱해서 더해주기
        # 예시-2.004은 2*(0.001^0)+4*(0.001^1) 이런식으로
        
        sijak.append(timestamp-timestamp2+0.001) # 시작시간은 완료시간에서 처리시간을 뺀 다음 처리시간이 시작시간 및 끝시간을 포함하므로 0.001초를 더해준 값
        kut.append(timestamp) # 완료시간은 그냥 그대로 넣기

    for i in range(len(lines)): # 각 요청을 읽어들이면서(lines,sijak,kut의 인덱스는 동일)
        count = 0 # 초당 최대처리량
        kijun = kut[i] # 최대처리량 측정 기준시각은 해당 요청이 끝나는 시각-탐욕 알고리듬의 최선 선택
        for j in range(i,len(lines)): # 해당 요청 다음의 것들을 읽어들이면서
            if sijak[j]<kijun+1: # 각 요청의 시작시각이 기준시각으로부터 1초 내에 있을경우-즉 기준시간 내에 요청이 포함될 시
                count+=1 # 최대처리량 하나씩 더하기
        answer = max(answer,count) # answer(이전 count값)및 count(현재)를 비교하여 더 큰것을 answer값으로
        
    return answer

사실 탐욕 외에도 동적 프로그래밍(DP), 완전 탐색(노가다) 같은 여러 방법이 있는데 어느 알고리듬을 써야 하는지는 그때그때 다르다. ↩︎
그럼 그렇지 않을 때는? 동적 프로그래밍(DP)라는 방법이 있다. 이건 다음에. ↩︎
시간을 정수형으로 나타내는 형태 ↩︎
요청시간은 시작과 끝을 포함하기 때문에 ↩︎

알고리듬

algorithm greedy

This post is licensed under CC BY 4.0 by the author.