알고리듬 문제를 풀어보자-dfs
알고리듬 문제를 풀어보자-dfs
시작하면서
이번에는 알고리듬 문제를 풀어보겠다.
알고리듬은 프로그래머의 기본 중 기본이기 때문이다.
비단 취업 준비뿐만이 아니라 회사 업무, 이직시에도 알고리듬 문제를 풀 줄 알아야 한다.
회사 업무평가나 경력직 채용도 코딩 테스트를 보기 때문이다…
다행히 학생 시절 미친듯한 과제 폭탄으로 알고리듬이라면 치가 떨리기에
알고리듬 포스트는 지금까지 학습한 내용을 상기시키고 문제를 풀어보며 응용하는 방식으로 써보려고 한다.
dfs 알고리듬
dfs는 깊이-우선-탐색이라는 의미로 그래프 내 모든 노드를 돌 때 쓰이는 가장 기본적인 알고리듬이다.
그래프가 뭐고, 노드가 뭐인지는 이제 설명하겠다.
그래프
- 그래프는 쉽게 말해 점들이 선으로 연결된 집합을 뜻한다.
- 점을 버텍스 또는 노드
- 선을 엣지라고 부른다.
- 먼저 점을 여러 개 찍는다. 그리고 점들을 선으로 연결한다. 연결되지 않는 점이 있어도 되고, 점 하나에 선을 몇 개든 연결할 수 있다. 자기 자신에도 선을 연결할 수 있다. 이렇게 하면 그래프 완성!
- 또한 엣지들에는 방향과 가중치라는 것이 존재할 수 있다.
- 방향은 ·->· 이런 그래프가 있을 때 왼쪽 노드에서 오른쪽 노드로는 갈 수 있지만, 그 반대는 안된다.
물론 양방향 엣지도 존재 가능하다. - 가중치는 엣지에 수 등을 부여하여 이 엣지로 이동하면 이정도의 비용이 든다, 를 선언하는 것이다.
눈치 챘겠지만, 보통 시작과 끝 노드를 주고 가장 적은 가중치로 이동하세요 등에 사용된다.
- 방향은 ·->· 이런 그래프가 있을 때 왼쪽 노드에서 오른쪽 노드로는 갈 수 있지만, 그 반대는 안된다.
- 그래프 탐색은 그래프 안의 버텍스들을 찾는 알고리듬이다.
- 크게 모든 버텍스를 찾는 알고리듬, 시작과 끝 버텍스를 주고 둘 사이를 가장 적은 엣지로 찾아가는 알고리듬이 존재한다.
- 이게 무슨 쓸모가 있나 생각하기 쉽지만, 활용 범위는 무궁무진하다. 가장 대표적인 예로는 게임 분야를 들 수 있다.
- GTA나 사이버펑크 같은 오픈-월드 게임에서는 도시의 생동감을 표현하기 위해 내비게이션 기능이 필요한데, 이 때 이러한 그래프 탐색 알고리듬이 활용되는 것이다.1
- dfs 알고리듬은 미로 찾기같이 경로를 일일이 찾아봐야 하는 경우에 주로 사용된다.
인접배열와 인접행렬
- dfs 알고리듬을 풀기 위해서는 인접 배열(인접 리스트)와 인접 행렬이라는 개념을 알아야 한다. 이 들은 버텍스 간의 연결관계를 수학적으로 표현하는 방법이다.
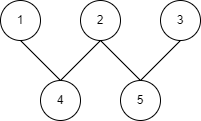
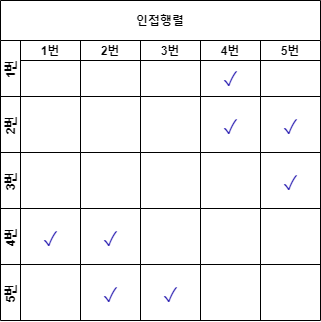
이러한 그래프가 있다고 보자. 올림픽도 막 끝난 만큼 오륜기 모양으로 만들어봤다.
동그라미는 버텍스(노드), 선은 양방향 엣지이다.- 1번 노드에는 4번 노드가, 2번 노드에는 4번 노드와 5번 노드가 연결되어 있다.
- 이렇게 각 노드마다 연결된 노드들을 행렬로 표현하면 인접 행렬, 배열로 표현하면 인접 배열이다.
- 그럼 어떻게 표현할 것인가. 쉽게 생각하면 된다.
- 인접 행렬
- 행과 렬 개수가 각각 노드 개수인 행렬을 만든다.
- 각 행과 렬을 노드 번호로 생각하고, 행 노드마다 연결된 노드 번호를 찾아 그 번호의 렬을 체크해주면 된다.
- 그러면 위 그래프를 인접 행렬로 표현해보면
이렇게 되겠지? - 참고로 자기 자신끼리는 체크하지 않는다. 즉 1열 1행, 2열 2행,… 등은
굳이 이렇게 자기 스스로 연결되어 있지 않는 이상 체크 안한다.
- 인접 배열
- 인접 행렬은 위 그림처럼 2차원적으로 표현하지만, 인접 배열은 1차원으로 표현한다.
- 무슨 말이냐면…
- 먼저 요소 개수가 노드 개수인 빈 리스트를 만든다.
int injop = new int[5] - 각 요소의 인덱스는 노드 번호라고 생각한다.
injop = [1번,2번,3번,4번,5번] - 각 요소의 값은 해당하는 노드 번호에 연결된 노드 번호 리스트이다.
injop = [[4],[4,5],[5],[2,5],[2,3]]
- 먼저 요소 개수가 노드 개수인 빈 리스트를 만든다.
dfs의 기본원리
- 이제 모든 사전준비가 끝났다. 드디어 dfs가 뭔지를 알 수 있다.
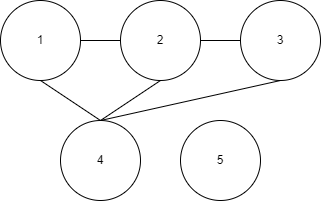
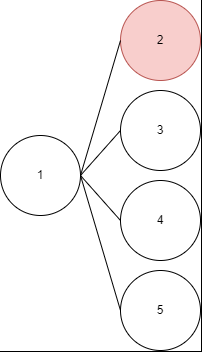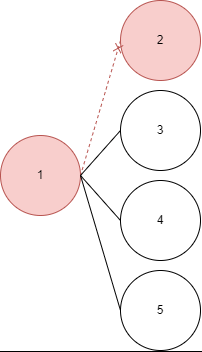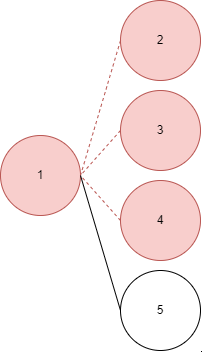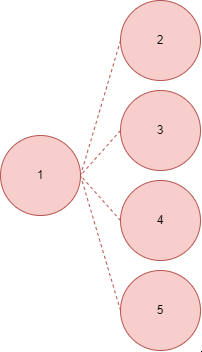
이번에는 이렇게 생긴 그래프를 예제로 든다. - dfs를 푸는 방법은…
- 우선 시작 노드를 정한다.
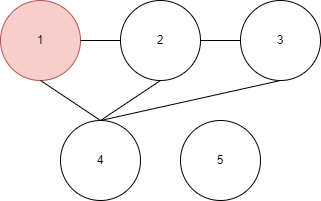
- 탐색한 노드에 체크를 한다. 당연히 시작 노드는 맨 처음 탐색하므로 체크한다.
여기서는 체크 표시로 빨간칠을 하겠다. - 이제 노드를 이동한다. 시작 노드와 연결된 노드를 이동한다.
이동한 노드를 나타내기 위해 시작 노드와 이동한 노드 간 엣지에 점선표시를 하겠다.
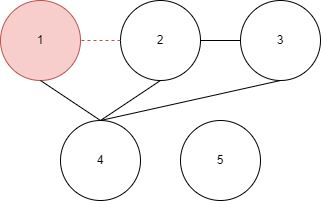
만약 연결 노드가 여러개면 특정 순서대로 이동한다. 여기서는 오름차순으로 이동한다. - 이제 이동한 노드를 시작 노드로 정한 뒤 1~3을 반복한다.
이 때, 3번에서 이동할 노드가 체크된 노드일 경우 이동하지 않는다.
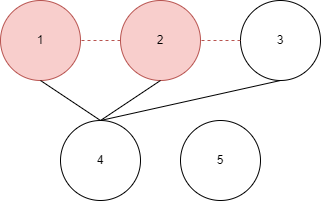
즉 여기서는 2번 노드로 이동 후, 다시 연결된 노드를 오름차순으로 탐색한다.
그러면 1번->3번->4번 노드 순으로 이동할 텐데, 1번 노드는 이미 체크되었으므로 이동하지 않고,
그 다음 노드인 3번으로 이동한다. - 만약 연결된 모든 노드가 탐색되었을 경우 이동하기 전 노드에서 다시 시작한다. 당연히 시작 노드에서 이동할 수 없는 노드는 체크되지 않을 것이다.
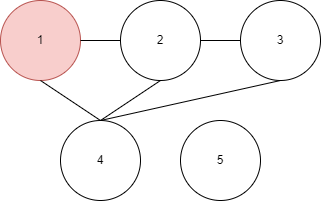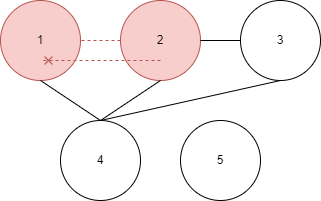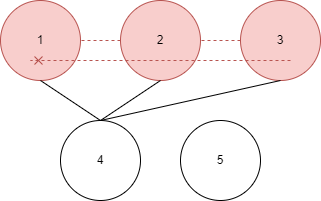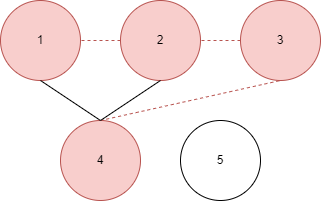
- 우선 시작 노드를 정한다.
- 이련 경우에는?
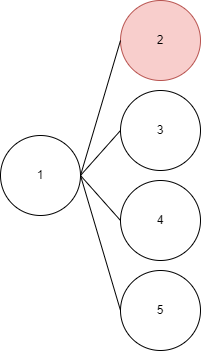
이렇게 하면 된다!
2번-1번-3번-4번-5번 순으로 탐색된다.
코드로 구현해보기
이제 이것을 C++ 코드로 구현해보자.
마침 acmicpc라는 사이트에 dfs 코드 구현 문제가 있다.
https://www.acmicpc.net/problem/24479
- 입력값 첫 줄로 노드 개수/엣지 개수/시작 노드번호 가 주어진다.
- 두번째 줄부터는 엣지 개수만큼 줄이 있다. 각 줄은 두 수 번호의 노드를 연결하는 엣지를 나타낸다.
- 시작 노드의 연결 노드를 오름차순으로 탐색한다.
- 출력의 각 줄은 노드 번호이다. 즉 첫번째 줄은 1번 노드
- 출력 줄의 값은 노드를 방문한 순서이다. 만약 시작 노드에서 탐색할 수 없으면 0으로 표기한다.
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int visited[100000];
int tosso[100000];
int atime=0;
void dfs(vector<int> a[], int r){
atime=atime+1;
visited[r-1] = 1;
tosso[r-1]=atime;
for(int i=0;i<a[r-1].size();i++){
if (visited[a[r-1][i]-1]==0){
dfs(a,a[r-1][i]);
}
}
}
int main(void){
int a,b,c;
cin>>a>>b>>c;
vector<int> table[a];
for(int i=0;i<b;i++){
int d,e;
cin>>d>>e;
table[d-1].push_back(e);
table[e-1].push_back(d);
}
for(int i=0;i<a;i++){
sort(table[i].begin(),table[i].end());
}
dfs(table,c);
for(int i=0;i<a;i++){
cout<<tosso[i]<<endl;
}
return 0;
}
일단 정답부터 표기하겠다. 차근차근 알아보자.
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int visited[100000];
int tosso[100000];
int atime=0;
전역변수 선언문 이다.
- 입출력값을 읽기 위해 iostream, 가변배열 자료형을 사용하기 위해 vector, 오름차순 정렬을 하기 위해 algorithm을 불러온다.
- 일일이 std:: 이렇게 입력해주지 않기 위해 std 네임스페이스를 미리 불러온다.
- 그 다음,
- 노드 체크 여부가 담겨있는 visited
- 방문 순서가 담겨있는 tosso
- 방문 순서 변수인 atime을 선언한다.
- visited와 tosso의 인덱스를 노드 번호-1로 취급한다. 따라서 visited[0]은 1번 노드의 체크 여부일 것이다.
- 또한 두 배열의 길이는 문제에서 최대 노드가 100000개라 하여으므로 100000으로 미리 선언해준다.
int main(void){
int a,b,c;
cin>>a>>b>>c;
vector<int> table[a];
for(int i=0;i<b;i++){
int d,e;
cin>>d>>e;
table[d-1].push_back(e);
table[e-1].push_back(d);
}
for(int i=0;i<a;i++){
sort(table[i].begin(),table[i].end());
}
dfs(table,c);
for(int i=0;i<a;i++){
cout<<tosso[i]<<endl;
}
return 0;
}
이제 main함수이다.
- a/b/c는 노드 개수/엣지 개수/시작노드 번호로 입력값에서 받는다.
- 그 다음 인접 리스트 table을 선언한다.
- table은 노드에 연결되어 있는(엣지가 있는) 노드들을 의미한다.
vector<int> table[a]이기 때문에 table은 a개의 요소가 있고, 각 요소의 형식은 vector라는 가변 배열이다.- table의 인덱스도 visited, tosso와 마찬가지로 노드 번호-1이다.
b번만큼 for문을 돌려
- 각 엣지에 연결되어 있는 노드 두개를 d/e로 받는다.
- d 번호에 해당하는 table 인덱스 값에 e를, e 번호에 해당하는 table 인덱스값에 d를 추가한다.
따라서 만약 입력값이
1 2 3 4 5 6
5 5 1 1 4 1 2 2 3 2 4 3 4
이면 table은
1
[[4,2],[1,3,4],[2,4],[1,2,3],[]]
이 될 것이다.
table을 만드면 오름차순 탐색을 위해 각 요소를 sort를 사용해 정렬한다.
1
[[2,4],[1,3,4],[2,4],[1,2,3],[]]
- 이제 이 table과 시작 번호(c)를 인자로 dfs 함수를 실행시킨다.
void dfs(vector<int> a[], int r){
atime=atime+1;
visited[r-1] = 1;
tosso[r-1]=atime;
for(int i=0;i<a[r-1].size();i++){
if (visited[a[r-1][i]-1]==0){
dfs(a,a[r-1][i]);
}
}
}
dfs 함수이다. a가 아까 받은 인접리스트, r은 시작노드 번호이다.
- dfs 함수를 한번 할 때마다 atime을 1씩 더해준다.
- 또한 시작 노드는 탐색하였으므로 visited의 시작노드 인덱스 값을 1로 바꿔준다.
- 똑같은 이유로 tosso의 같은 인덱스 값도 atime으로 바꿔 준다.
- for문을 사용해 인접리스트의 시작 노드 인덱스 값들을 탐색한다.
- 즉 1번 인덱스이면 for문은 [2,4] 를 탐색할 것이다. 이 값이 바로 연결된 노드들이다.
- 만일 이 노드값-1을 인덱스로 하는 visited 값이 0이라면, 즉 탐색하지 않았다면
- 이 노드값을 시작 노드로 하여 dfs 함수를 재귀한다.
- 반대로 visited 값이 1이면 아무것도 하지 않고 다음 값으로 이동한다.
즉 위에서 말한 체크된 노드는 탐색하지 않는다 을 하는 것이다. - 따라서 visited[1]=1이고 visited[3]=0 이면 2번 노드는 탐색하지 않고, 4번 노드는 재귀를 사용해 탐색할 것이다.
- 그러므로 실행 순서를 정리하자면
- 1번 노드에서 시작하므로 인접리스트에서 찾은 2,4번 노드를 탐색한다.
- 2번 노드는 탐색하지 않았으므로(
visited[1]=1) 2번 노드를 시작노드로 하여 인접리스트 값인 [1,3,4]를 탐색한다. - 1번 노드는 탐색하였으므로 3번 노드를 시작노드로 하여 인접리스트 값인 [2,4]를 탐색
- 마찬가지로 2번 노드도 탐색하였으므로 4번 노드를 시작노드로 하여 [1,2,3] 탐색
- 1,2,3번 노드 모두 탐색하였으므로 재귀 해제, 3번 노드가 시작노드인 dfs로 이동
- 3번 노드도 2,4번 모두 탐색하였으므로 재귀 해제, 2번 노드 dfs로 이동
- 2번 노드도 모두 탐색하였으므로 재귀 해제, 맨 처음인 1번 노드 dfs로 이동
- 마찬가지로 모두 탐색하였으므로 dfs 함수가 끝난다.
acmicpc 문제풀이 주의점
- 다만 위 코드를 그대로 문제에 붙여쓰면 시간 초과가 발생한다.
- 분명히 이론적으로 맞는 코드인데, 본인도 이 문제를 해결하려 몇 시간을 쏟아부었다.
무수한 시간초과의 향연… - 처음에는 정렬시 시간복잡도 문제, 리스트 탐색 시간문제 등인줄 알았으나, 의외로 해결법은 간단했다.
- 그냥 입출력 함수 cin/cout이 시간을 많이 잡아먹기 때문이었다.
이를 해결하기 위해서는 약간의 편법이 필요하다.
main함수 맨 앞에
ios_base :: sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);이 코드를 써 준다.
- 주의-절대 실전 프로그램에서는 사용하지 마시오
- cout의 endl을 ‘\n’으로 바꿔준다.
- 가장 좋은 방법으로는 cin/cout 대신 printf(),scanf()를 사용한다.
- 이렇게 하면 입출력 속도가 매우 빨라진다.
- 자세하게는 모르겠지만, cin/cout 의 시스템 버퍼 동기화를 해제하는 원리라고 한다.
- 되도록이면 acimcpc에서 문제를 풀때는 cin/cout 대신 printf()와 scanf()를 쓰도록 하자.
- 물론 include iostream 대신 cstdio를 해야 한다.
이런 복잡한 게임에서는 더 고도화된 방식인 최단 거리 탐색을 사용한다. 벨만-포드 알고리듬, 플로이드-와셔 알고리듬 등 여러 방식이 있는데, 시간 나면 설명하겠다. ↩︎
This post is licensed under CC BY 4.0 by the author.